Un puñado de mónadas

La primera vez que hablamos de los funtores, vimos que son un concepto útil para los valores que se pueden mapear. Luego, llevamos ese concepto un poco más lejos y vimos los funtores aplicativos, que nos permite ver los valores de ciertos tipos de datos como una especia de valores con un contexto de forma que podemos aplicar funciones normales sobre ellos mantenido dicho contexto.

En este capítulos hablaremos de las mónadas, que simplemente son una versión ampliada de los funtores aplicativos, de la misma forma que los funtores aplicativos son una versión ampliada de los funtores.

Cuando hablamos de los funtores vimos que es era posible mapear funciones sobre varios tipos de datos. Para lograrlo utilizábamos la clase de tipos Functor. Dada una función del tipo a -> b y un dato del tipo f a nos preguntábamos cómo mapeamos esta función sobre el dato de forma que obtuviésemos un resulto con el tipo f b. Vimos como mapear funciones sobre datos del tipo Maybe a, del tipo [a], IO a, etc. Incluso vimos como mapear funciones a -> b sobre funciones r -> a de forma que el resultado daba funciones del tipo r -> b. Para contestar a la pregunta que nos hacíamos de como mapear una función sobre un dato, lo único que tenemos que hacer es mirar el tipo de fmap:

fmap :: (Functor f) => (a -> b) -> f a -> f b

Y luego hacer que funcione con el tipo de datos para el que estamos creando la instancia de Functor.

Luego vimos que era posible mejorar los funtores. Decíamos: ¡Hey! ¿qué pasa si tenemos una función a -> b dentro del valor de un funtor? Como por ejemplo, Just (*3), y queremos aplicarla a Just 5. ¿Qué pasaría si en vez de aplicarla a Just 5 la aplicamos a Nothing? ¿O si tenemos [(*2),(+4)] y queremos aplicarla a [1,2,3]? ¿Cómo hacemos para que funcione de forma general? Para ello utilizamos la clase de tipos Applicative.

(<*>) :: (Applicative f) => f (a -> b) -> f a -> f b

También vimos que podíamos tomar un valor normal e introducirlo dentro de un tipo de datos. Por ejemplo, podemos tomar un 1 en introducirlo en un tipo Maybe de forma que resulte en Just 1. O incluso podríamos crear un [1]. O una acción de E/S que no realizara nada y devolviera un 1. La función que realiza esta acción es pure.

Como ya dijimos, un valor aplicativo puede verse como un valor dentro de un contexto. Un valor adornado en términos técnicos. Por ejemplo, el carácter 'a' es un simple carácter normal, mientras que Just 'a' tiene añadido un cierto contexto. En lugar de un Char tenemos un Maybe Char, que nos dice que su valor puede ser un carácter o bien la ausencia de un carácter.

También es genial ver como la clase de tipos Applicative nos permite utilizar funciones normales con esos contextos de forma que los contextos se mantengan. Observa:

ghci> (*) <$> Just 2 <*> Just 8
Just 16
ghci> (++) <$> Just "klingon" <*> Nothing
Nothing
ghci> (-) <$> [3,4] <*> [1,2,3]
[2,1,0,3,2,1]

Estupendo, ahora que los tratamos con valores aplicativos, los valores Maybe a representan cómputos que pueden fallar, [a] representan cómputos que tienen varios resultados (cómputos no deterministas), IO a representan valores que tienen efectos secundarios, etc.

Las mónadas son una extensión natural de los funtores aplicativos y tratan de resolver lo siguiente: si tenemos un valor en un cierto contexto, m a, ¿cómo podemos aplicarle una función que toma un valor normal a y devuelve un valor en un contexto? Es decir, ¿cómo podemos aplicarle una función del tipo a -> m b? Básicamente lo que queremos es esta función:

(>>=) :: (Monad m) => m a -> (a -> m b) -> m b

Si tenemos un valor adornado y una función que toma un valor y devuelve un valor adornado, ¿cómo pasamos el primer valor adornado a la función?. Esta será la pregunta principal que nos haremos cuando trabajemos con las mónadas. Escribimos m a en lugar de f a ya que m representa mónadas, aunque las mónadas no son más que funtores aplicativos que soportan la función >>=. Llamamos lazo a la función >>=.

Cuando tenemos un valor normal a y una función normal a -> b es muy fácil pasar ese valor a la función. Simplemente hay que aplicar la función a ese valor de forma normal. Pero cuando estamos trabajando con valores que vienen dentro de un cierto contexto, tenemos que tomarnos un tiempo para ver como estos valores adornados se pasan a las funciones y para ver como se comportan. No te preocupes, verás que es muy fácil.

Manos a la obra con Maybe

Ahora que ya tenemos una pequeña idea del cometido de la mónadas, vamos a expandirla en detalle.

Para sorpresa de nadie, Maybe es una mónada, así que vamos a explorarlo un poco más a ver si podemos combinar lo que ya sabemos con las mónadas.

Nota

Llegados a este punto, asegúrate de que entiendes los funtores aplicativos. Será más fácil si sabes como funcionan varias instancias de Applicative y que tipo de cómputos representan, ya que las mónadas no son más que una expansión de los funtores aplicativos.

Un valor de tipo Maybe a representa un valor del tipo a dentro del contexto de que ocurra un posible fallo. Un valor Just "dharma" representa que la cadena "dharma" está presente mientras que Nothing representa su ausencia, o si vemos la cadena como el resultado de un cómputo, significará que dicho cómputo ha fallado.

Cuando hablamos de Maybe como funtor vimos que cuando mapeamos una función sobre él con fmap, se mapea solo cuando es un valor Just, de otro modo Nothing se mantiene como resultado ya que no hay nada sobre lo que mapear.

Como esto:

ghci> fmap (++"!") (Just "wisdom")
Just "wisdom!"
ghci> fmap (++"!") Nothing
Nothing

Como funtor aplicativo funciona de forma similar. Sin embargo, los funtores aplicativos también poseen funciones dentro de los funtores. Maybe es un funtor aplicativo de forma que cuando aplicamos <*> con una función contenida en un Maybe a un valor contenido en un Maybe, ambos deben ser valores Just para que el resultado sea también un valor Just, en caso contrario el resultado será Nothing. Tiene sentido ya que si no tenemos o bien la función o bien el valor, no podemos crear un resultado a partir de la nada, así que hay que propagar el fallo:

ghci> Just (+3) <*> Just 3
Just 6
ghci> Nothing <*> Just "greed"
Nothing
ghci> Just ord <*> Nothing
Nothing

Cuando utilizamos el estilo aplicativo con funciones normales para que actúen con valores del tipo Maybe es similar. Todos los valores deben ser Just si queremos que el resultado también lo sea.

ghci> max <$> Just 3 <*> Just 6
Just 6
ghci> max <$> Just 3 <*> Nothing
Nothing

Y ahora vamos a ver como podríamos implementar >>= para Maybe. Como ya hemos dicho, >>= toma un valor monádico y una función que toma un valor normal y devuelve otro valor monádico, de forma que aplica esta función al valor monádico. ¿Cómo consigue hacerlo si la función solo toma valores normales? Bueno, para lograrlo hay que tomar en cuenta el contexto de ese valor monádico.

En este caso, >>= tomará un valor con el tipo Maybe a y una función de tipo a -> ``Maybe b y de alguna forma aplicará esta función para dar como resultado Maybe b. Para imaginarnos como se hace, podemos apoyarnos en lo que ya sabemos de los funtores aplicativos. Digamos que tenemos una función del tipo \x -> Just (x+1). Toma un número, le añade 1 y lo introduce en un Just:

ghci> (\x -> Just (x+1)) 1
Just 2
ghci> (\x -> Just (x+1)) 100
Just 101

Si le pasaramos como parámetro 1 devolvería Just 2. Si le pasaramos 100 devolvería Just 101. Simple. Ahora viene lo bueno: ¿cómo pasamos un dato del tipo Maybe a esta función? Si pensamos en Maybe como un funtor aplicativo contestar a esta pregunta es bastante fácil. Si le pasamos un valor Just, toma el valor que contiene y le aplica la función. Si le pasamos Nothing, mmm, bueno, tenemos la función pero no tenemos nada que pasarle. En este caso vamos a hacer lo mismo que hicimos anteriormente y diremos que el resultado será Nothing.

En lugar de llamar a esta función >>=, vamos a llamarla applyMaybe por ahora. Toma un Maybe a y una función que devuelve un Maybe b y se las ingenia para aplicar esa función a Maybe a. Aquí está la función:

applyMaybe :: Maybe a -> (a -> Maybe b) -> Maybe b
applyMaybe Nothing f  = Nothing
applyMaybe (Just x) f = f x

Vale, ahora vamos a jugar un poco con ella. La utilizamos de forma infija de forma que el valor Maybe estará en la parte izquierda y la función a aplicar en la parte derecha:

ghci> Just 3 `applyMaybe` \x -> Just (x+1)
Just 4
ghci> Just "smile" `applyMaybe` \x -> Just (x ++ " :)")
Just "smile :)"
ghci> Nothing `applyMaybe` \x -> Just (x+1)
Nothing
ghci> Nothing `applyMaybe` \x -> Just (x ++ " :)")
Nothing

En este ejemplo vemos que cuando utilizamos applyMaybe con un valor Just y una función, la función simplemente se aplica al valor contenido en Just. Cuando la utilizamos con un valor Nothing, el resultado final es Nothing. ¿Qué pasa si la función devuelve un Nothing? Vamos ver:

ghci> Just 3 `applyMaybe` \x -> if x > 2 then Just x else Nothing
Just 3
ghci> Just 1 `applyMaybe` \x -> if x > 2 then Just x else Nothing
Nothing

Justo como imaginábamos. Si el valor monádico de la izquierda es Nothing, el resultado final es Nothing. Y si la función de la derecha devuelve Nothing, el resultado será de nuevo Nothing. Es muy parecido a cuando utilizabamos Maybe como funtor aplicativo y obteniamos como resultado Nothing si en algún lugar había un Nothing.

Parace que para Maybe, hemos averiguado como tomar un valor decorado y pasarlo a una función que toma un parámetro normal y devuelve otro valor decorado. Lo hemos conseguido teniendo en cuenta que los valores del tipo Maybe representan cómputo que pueden fallar.

Seguramente te este preguntado: ¿y esto es útil? Puede parecer que los funtores aplicativos son más potentes que las mónadas, ya que los funtores aplicativos permiten tomar una función normal y hacer que opere sobre valores con un cierto contexto. Veremos que las mónadas pueden hacer exactamente lo mismo ya que son una versión mejorada de los funtores aplicativos, pero también veremos que pueden hacer más cosas que los funtores aplicativos no pueden hacer.

Volvermos con Maybe en un momento, pero primero, vamos a ver la clase de tipos que define las mónadas.

La clase de tipos de las mónadas

De la misma forma que los funtores tienen una clase Functor y que los funtores aplicativos tienen una clase Applicative, las mónadas vienen con su propia clase de tipos: Monad ¡Wau! ¿Quíen lo hubiera imaginado? Así es como luce su definición:

class Monad m where
    return :: a -> m a

    (>>=) :: m a -> (a -> m b) -> m b

    (>>) :: m a -> m b -> m b
    x >> y = x >>= \_ -> y

    fail :: String -> m a
    fail msg = error msg

Empecemos por la primera línea. Dice class Monad m where. Pero espera, ¿no hemos dicho que las mónadas no son más que funtores aplicativos ampliados? ¿No debería haber una resitricción de clase como class (Applicative m) = > Monad m where de forma que el tipo tenga que ser un funtor aplicativo primero antes de ser una mónada? Bueno, debería, pero cuando se creo Haskell, la gente que lo creo no pensó que los funtores aplicativos encajarían bien en Haskell así que no aparece. Pero ten seguro que cada mónada es un funtor aplicativo, incluso aunque la declaración de la clase Monad diga lo contrario.

La primera función que define la clase de tipos Monad es return. Es lo mismo que pure pero con un nombre diferente. Su tipo es (Monad m) => a -> m a. Toma un valor y lo introduce en el contexto por defecto que pueda albergar dicho valor. En otras palabras, toma un valor y lo introduce en una mónada. Siempre hace lo mismo que la función pueda de la clase de tipos Applicative, por lo que ya estmos familiarizados al uso de return. Ya hemos utilizado return cuando trabajamos con la E/S. La utilizabamos para crear una acción de E/S que no hiciera nada salvo contener un valor. Con Maybe toma un valor y lo introduce en un valor Just.

Nota

Recordatorio: return no se parece en nada al return de la mayoría de los otro lenguajes de programación. No termina la ejecución ni nada por el estilo, simplemente toma un valor normal y lo introduce en un contexto.

La siguiente función es >>= o lazo. Es como la aplicación de funciones, solo que en lugar de tomar un valor y pasarlo a una función normal, toma un valor monádico (es decir, un valor en un cierto contexto) y lo pasa a una función que toma un valor normal pero devuelve otro valor monádico.

A continuación tenemos >>. No le vamos a prestar mucha ateción ahora mismo ya que viene con una implementación por defecto y prácticamente nunca tendremos que implementarla cuando creemos instancias de Monad.

La función final de la clase de tipos Monad es fail. Nunca la utilizaremos explícitamente en nuestro código. En cambio, Haskell la utilizará para permitir fallos en una construción sintáctica para las mónadas que veremos más adelante. No tenemos que preocuparnos demasiado con fail ahora mismo.

Ahora que ya sabemos como luce la clase de tipos Monad, vamos a ver como es la instancia de Maybe para la clase Monad:

instance Monad Maybe where
    return x = Just x
    Nothing >>= f = Nothing
    Just x >>= f  = f x
    fail _ = Nothing

return es lo mismo que pure, no hay que pensar mucho. Hacemos exactamente lo mismo que hacíamos con Applicative, introducimos un valor en Just.

La función >>= es exactamente igual applyMaybe. Cuando le pasamos un valor del tipo Maybe a a esta función, tenemos en cuenta el contexto y devolvemos Nothing si el valor a la izquierda es Nothing ya que no existe forma posible de aplicar la función con este valor. Si es un valor Just tomamos lo que hay dentro de él y aplicamos la función.

Podemos probar un poco Maybe como mónada:

ghci> return "WHAT" :: Maybe String
Just "WHAT"
ghci> Just 9 >>= \x -> return (x*10)
Just 90
ghci> Nothing >>= \x -> return (x*10)
Nothing

Nada nuevo o emocionante en la primera línea ya que ya hemos usado pure con Maybe y sabemos que return es igual que pure solo que con otro nombre. La siguientes dos líneas muestran como funciona >>= un poco más.

Fíjate en como hemos pasado Just 9 a la función \x -> return (x*10), x toma el valor 9 dentro de la función. Parece como si fueramos capaces de extraer el valor de un Maybe sin utilizar un ajuste de patrones. Y aún así no perdemos el contexto de los tipo Maybe, porque cuando es Nothing, el resultado de >>= será Nothing también.

En la cuerda floja

Ahora que ya sabemos como parar un valor del tipo Maybe a a una función del tipo a -> Maybe b teniendo en cuenta el contexto de un posible fallo, vamos a ver como podemos usar >>= repetidamente para manejar varios valores Maybe a.

Pierre ha decidido tomar un descanso en su trabajo en la piscifactoria e intentar caminar por la cuerda floja. No lo hace nada mal, pero tiene un problema: ¡los pájaros se posan sobre su barra de equilibrio! Aterrizan y se toman un pequeño respiro, hablan con sus respectivos amigos ovíparos y luego se marchan en busca de algo de comida. Ha Pierre no le importaría demasiado si el número de pájaros que se posan en cada lado de la barra fuera el mismo. Sin embargo, a menudo, todos los pájaros se posan en el mismo lado y desequilibran a Pierre tirándolo de la cuerda de forma embarazosa (utiliza un red de seguridad obviamente).

Digamos que matiene el equilibrio si el número de pájaros posados a la izquierda y a la derecha de la barra no difere en más de tres. Así que si hay un pájaro en la parte derecha y otros cuatro pájaros en la parte izquierda no pasa nada. Pero si un quinto pájaro aterriza en la parte derecha pierde el quilibrio y cae.

Vamos a simular un grupo de pájaros que aterrizan o inician el vuelo desde la barra y ver si Pierre sigue sobre la barra tras un número de eventos relacionados con estas aves. Por ejemplo, queremos saber que le pasará a Pierre si primero llega un pájaro al lado izquierdo de la barra, luego cuatro pájaros más se posan sobre la parte derecha y luego el pájaro de la izquierda decide volar de nuevo.

Podemos representar la barra con un par de enteros. El primer componente indicará el número de pájaros a la izquierda mientras que el segundo indicará el número de pájaros de la derecha:

type Birds = Int
type Pole = (Birds,Birds)

Primero creamos un sinónimo para Int, llamado pájaros (Birds), ya que estamos utilizando enteros para representar el número de pájaros. Luego creamos otro sinónimo de tipos (Birds, Birds) y lo llamamos barra (Pole).

A continuación creamos una función que toma un número de pájaros y los posa sobre un determinado lado de la barra. Aquí están las funciones:

landLeft :: Birds -> Pole -> Pole
landLeft n (left,right) = (left + n,right)

landRight :: Birds -> Pole -> Pole
landRight n (left,right) = (left,right + n)

Bastante simple. Vamos a probarlas:

ghci> landLeft 2 (0,0)
(2,0)
ghci> landRight 1 (1,2)
(1,3)
ghci> landRight (-1) (1,2)
(1,1)

Para hacer que los pájaros vuelen simplemente tenmos que pasarles a estas funciones un número negativo. Como estas funciones devuelven un valor del tipo Pole, podemos encadenarlas:

ghci> landLeft 2 (landRight 1 (landLeft 1 (0,0)))
(3,1)

Cuando aplicamos la función landLeft 1 a (0, 0) obtenemos (1, 0). Luego aterrizamos un pájaro sobre el lado derecho, por lo que obtenemos (1, 1). Para terminar aterrizamos dos pájaros más sobre el lado izquierdo, lo cual resulta en (3, 1). Aplicamos una función a algo escribirendo primero el nombre de la función y luego sus parámetros, pero en este caso sería mejor si la barra fuera primero y luego las funciones de aterrizar. Si creamos una función como:

x -: f = f x

Podríamos aplicar funciones escribiendo primero el parámetro y luego el nombre de la función:

ghci> 100 -: (*3)
300
ghci> True -: not
False
ghci> (0, 0) -: landLeft 2
(2,0)

Utilizando esto podemos aterrrizar varios pájaros de un forma mucho más legible:

ghci> (0, 0) -: landLeft 1 -: landRight 1 -: landLeft 2
(3,1)

¡Genial! Es ejemplo es equivalente al ejemplo anterior en el que aterrizamos varias aves en la barra, solo que se ve más limpio. Así es más obvio que empezamos con (0, 0) y luego aterrizamos un pájaro sobre la izquierda, otro sobre la derecha y finalmente dos más sobre la izquierda.

Hasta aquí bien, pero, ¿qué sucede si aterrizan diez pájaros sobre un lado?

ghci> landLeft 10 (0,3)
(10,3)

¿Diez pájaros en la parte izquierda y solo tres en la derecha? Seguro que Pierre ya debe estar volando por los aires en esos momentos. En este ejemplo es bastante obvio pero, ¿y si tenemos una secuencia como esta?:

ghci> (0,0) -: landLeft 1 -: landRight 4 -: landLeft (-1) -: landRight (-2)
(0,2)

A primera vista puede parecer que todo esta bien pero si seguimos los pasos, veremos que en un determinado momento hay cuatro pájaros a la derecha y ninguno a la izquierda. Para arreglar esto debemos darle una vuelta de tuerca a las funciones landLeft y landRight. A partir de lo que hemos aprendido queremos que estas funciones sean capaces de fallar. Es decir, queremos que devuelvan una barra si Pierre consigue mantener el equilibrio pero que fallen en caso de que Pierre lo pierda. ¡Y qué mejor manera de añadir el contexto de un posible fallo a un valor que utilizar Maybe! Vamos a reescribir estas funciones:

landLeft :: Birds -> Pole -> Maybe Pole
landLeft n (left,right)
    | abs ((left + n) - right) < 4 = Just (left + n, right)
    | otherwise                    = Nothing

landRight :: Birds -> Pole -> Maybe Pole
landRight n (left,right)
    | abs (left - (right + n)) < 4 = Just (left, right + n)
    | otherwise                    = Nothing

En lugar de devolver un Pole estas funciones devuelven un Maybe Pole. Siguen tomando el número de pájaros y el estado de la barra anterior, pero ahora comprueban si el número de pájaros y la posición de estos es suficiente como para desquilibrar a Pierre. Utilizamos guardas para comprabar si diferencia entre el número de pájaros en cada lado es menor que cuatro. Si lo es devuelve una nueva barra dentro de un Just. Si no lo es, devuelven Nothing.

Vamos a jugar con estas pequeñas:

ghci> landLeft 2 (0,0)
Just (2,0)
ghci> landLeft 10 (0,3)
Nothing

¡Bien! Cuando aterrizamos pájaros sin que Pierre pierda el equilibrio obtenemos una nueva barra dentro de un Just. Pero cuando unos cunatos pájaros de más acaban en un lado de la barra obtenemos Nothing. Esto esta muy bien pero ahora hemos perido la posibilidad de aterrizar pájaros de forma repetiva sobre la barra. Ya no podemos usar landLeft 1 (landRight 1 (0,0)) ya que cuando aplicamos landRight 1 a (0, 0) no obtenemos un Pole, sino un Maybe Pole. landLeft 1 toma un Pole y no un Maybe Pole.

Necesitamos una forma de tomar un Maybe Pole y pasarlo a una función que toma un Pole y devuelve un Maybe Pole. Por suerte tenemos >>=, que hace exáctamen lo que buscamos para Maybe. Vamos a probarlo:

ghci> landRight 1 (0,0) >>= landLeft 2
Just (2,1)

Recuerda, landLeft 2 tiene un tipo Pole -> Maybe Pole. No podemos pasarle directamente un valor del tipo Maybe Pole que es el resultado de landRight 1 (0, 0), así que utilizamos >>= que toma un valor con un determinado contexto y se lo pasa a landLeft 2. De hecho >>= nos permite tratar valores Maybe como valores en un contexto si pasamos Nothing a landLeft 2, de forma que el resultado será Nothing y el fallo ser propagará:

ghci> Nothing >>= landLeft 2
Nothing

Gracias a esto ahora podemos encadenar varios aterrizajes que pueden consguir tirar a Pierre ya que >>= nos permite pasar valores monádicos a funciones que toman valores normales.

Aquí tienes una secuencia de aterrizajes:

ghci> return (0,0) >>= landRight 2 >>= landLeft 2 >>= landRight 2
Just (2,4)

Al principio hemos utilizado return para insertar una barra dentro de un Just. Podríamos haber aplicado landRight 2 directamente a (0, 0), hubiéramos llegado al mismo resultado, pero de esta forma podemos utilizar ``>>= para cada función de forma más consistente. Se pasa Just (0, 0) a landRight 2, lo que devuelve Just (0, 2). Luego se le pasa este valor a landLeft 2 obteniendo Just (2, 2) y así sucesivamente.

Recuerda el ejemplo que dijimos que tiraría a Pierre:

ghci> (0,0) -: landLeft 1 -: landRight 4 -: landLeft (-1) -: landRight (-2)
(0,2)

Como vemos no simula la interacción con las aves correctamente ya que en medio la barra ya estaría volando por los aires pero el resultado no lo refleja. Pero ahora vamos a probar a utilizar la aplicación monádica (>>=) en lugar de la aplicación normal:

ghci> return (0,0) >>= landLeft 1 >>= landRight 4 >>= landLeft (-1) >>= landRight (-2)
Nothing

Perfecto. El resultado final representa un fallo, que es justo lo que esperamos. Vamos a ver como se consigue este resultado. Primero, return introduce (0, 0) en el contexto por defecto, convirtiéndolo en Just (0, 0). Luego sucede Just (0,0) >>= landLeft 1. Como Just (0,0) es un valor Just, landLeft 1 es aplicado a (0, 0), obteniendo así Just (1, 0) ya que Pierre sigue manteniendo el equilibrio. Luego nos encontramos con Just (1,0) >>= landRight 4 lo cual resulta en Just (1, 4) ya que Pierre sigue manteniendo el equilibrio, aunque malamente. Se aplica landLeft (-1) a Just (1, 4), o dicho de otra forma, se computa landLeft (-1) (1,4). Ahora, debido a como funciona landLeft, esto devuelve Nothing porque nuestro esta volando por los aires en este mismo momento. Ahora que tenemos Nothing como resultado, éste se pasado a landRight (-2), pero como es un valor ``Nothing, el resultado es automáticamente Nothing ya que no existe ningún valor que se puede aplicar a landRight (-2).

No podíamos haber conseguido esto utilizando solo Maybe como funtor aplicativo. Si lo intentas te quedarás atascado, porque los funtores aplicativos no permiten que los valores aplicativos interactuen con los otros lo sufiente. Pueden, como mucho, ser utilizados como parámetros de una función utilizando el estilo aplicativo. Los operadores aplicativos tomarán los resultados y se los pasarán a la función de forma apropiada para cada funto aplicativo y luego obtendrán un valor aplicativo, pero no existe ninguna interacción entre ellos. Aquí, sin embargo, cada paso depende del resultado anterior. Por cada aterrizaje se examina el resultado anterior y se comprueba que la barra está balanceada. Esto determina si el aterrizaje se completará o fallará.

Podemos divisar una función que ignora el número de pájaros en la barra de equilibrio y simplemente haga que Pierre caiga. La llamaremos banana:

banana :: Pole -> Maybe Pole
banana _ = Nothing

Ahora podemos encadenar esta función con los aterrizajes de las aves. Siempre hara que Pierre se caiga ya que ignora cualquier cosa que se le pasa y devuelve un fallo. Compruebalo:

ghci> return (0,0) >>= landLeft 1 >>= banana >>= landRight 1
Nothing

El valor Just (1, 0) se le pasa a banana, pero este produce Nothing, lo cual hace que el resultado final sea Nothing. Menuda suerte.

En lugar de crear funciones que ignoren el resultado y simplemente devuelvan un valor monádico, podemos utilizar la función >> cuya implementación por defecto es esta:

(>>) :: (Monad m) => m a -> m b -> m b
m >> n = m >>= \_ -> n

Normalmente, si pasamos un valor a una función que toma un parámetro y siempre devuelve un mismo valor por defecto el resultado será este valor por defecto. En cambio con la mónadas también debemos conseiderar el contexto y el siguinificado de éstas. Aquí tienes un ejemplo de como funciona >> con Maybe:

ghci> Nothing >> Just 3
Nothing
ghci> Just 3 >> Just 4
Just 4
ghci> Just 3 >> Nothing
Nothing

Si reemplazamos >> por >>= \_ -> es fácil de ver lo que realmente sucede.

Podemos cambiar la función banana por >> y luego un Nothing:

ghci> return (0,0) >>= landLeft 1 >> Nothing >>= landRight 1
Nothing

Ahí lo tienes, ¡garantizamos que Pierre se va ir al suelo!

También vale la pena echar un vistazo a como se veria esto si no hubiesemos tratado los valores Maybe como valores en un contexto y no hubiersemos pasado las parámetros a las funciones como hemos hecho. Así es como se vería una serie de aterrizajes:

routine :: Maybe Pole
routine = case landLeft 1 (0,0) of
    Nothing -> Nothing
    Just pole1 -> case landRight 4 pole1 of
        Nothing -> Nothing
        Just pole2 -> case landLeft 2 pole2 of
            Nothing -> Nothing
            Just pole3 -> landLeft 1 pole3

Aterrizamos un pájaro y comprobamos la posibiliadad de que que ocurra un fallo o no. En caso de fallo devolvemos Nothing. En caso contrario aterrizamos unos cuantos pájaros más a la derecha y volemos a comprobar lo mismo una y otra vez. Convertir esto es un limpia concatenación de aplicaciones monádicas con >>= es un ejemplo clásico de porque la mónada Maybe nos ahorra mucho tiempo cuando tenemos una secuecnia de cómputos que dependen del resultado de otros cómputos que pueden fallar.

Fíjate en como la implementación de >>= para Maybe interpreta exactamente la lógica de que en caso encontrarnos con un Nothing, lo devolvemos como resultado y en caso contrario continuamos con lo que hay dentro de Just.

En esta sección hemos tomado varias funciones que ya teniamos y hemos visto que funcionan mejor si el valor que devuelven soporta fallos. Conviertiendo estos valores en valores del tipo Maybe y cambiando la aplicación de funciones normal por >>= obtenemos un mecanismo para manejar fallos casi de forma automática, ya que se supone >>= preserva el contexto del valor que se aplica a una función. En este caso el contexto que tenían estos valores era la posibiliadad de fallo de forma que cuando aplicábamos funciones sobre estos valores, la posibilidad de fallo siempre era tomada en cuenta.

La notación Do

Las mónadas son tan útiles en Haskell que tienen su propia sintaxis especial llamada notación do. Ya nos hemos topado con la notación do cuando reliazabamos acciones de E/S y dijimos que servia para unir varias de estas acciones en una sola. Bueno, pues resulta que la notación do no solo funciona con IO sino que puede ser utilizada para cualquier mónada. El principio sigue siendo el mismo: unir varios valores monádicos en secuencia. Vamos a ver como funiona la notación do y porque es útil.

Considera el siguiente ejemplo familiar de una aplicación monádica:

ghci> Just 3 >>= (\x -> Just (show x ++ "!"))
Just "3!"

Pasamos un valor monádico a una función que devuelve otro valor monádico. Nada nuevo. Fíjate que en el ejemplo anterior, x se convierte en 3, es decir, una vez dentro de la función lambda, Just 3 pasa a ser un valor normal en vez de un valor monádico. Ahora, ¿qué pasaría si tuviésemos otro >>= dentro de la función?

ghci> Just 3 >>= (\x -> Just "!" >>= (\y -> Just (show x ++ y)))
Just "3!"

¡Wau, un >>= anidado! En la función lambda interior, simplemente pasamos Just ! a \y -> Just (show x ++ y). Dentro de esta lambda, y se convierte en "!". x sigue siendo el 3 que obtuvimos de la lambda exterior. Esto se parece a la siguiente expresión:

ghci> let x = 3; y = "!" in show x ++ y
"3!"

La diferencia principal entre ambas es que los valores de la primera son valores monádicos. Son valores con el contexto de un posible fallo. Podemos remplazar cualquier valor por un fallo:

ghci> Nothing >>= (\x -> Just "!" >>= (\y -> Just (show x ++ y)))
Nothing
ghci> Just 3 >>= (\x -> Nothing >>= (\y -> Just (show x ++ y)))
Nothing
ghci> Just 3 >>= (\x -> Just "!" >>= (\y -> Nothing))
Nothing

En la primera línea, pasamos Nothing a una función y naturalmente resulta en Nothing. En la segunda línea pasamos Just 3 a la función de forma que x se convierte en 3, pero luego pasamos Nothing a la función lambda interior así que el resultado es también Nothing. Todo esto es parecido a ligar nombres con ciertos valores utilizando las expresiones let, solo que en lugar de valores normales son valores monádicos.

El siguiente ejemplo ilustra esta idea. Vamos a escribir lo mismo solo que cada valor Maybe esté en una sola línea:

foo :: Maybe String
foo = Just 3   >>= (\x ->
      Just "!" >>= (\y ->
      Just (show x ++ y)))

En lugar de escribir todos estas funciones lambdas, Haskell nos proporciona la sintaxis do que nos permite escribir el anterior trozo de código como:

foo :: Maybe String
foo = do
    x <- Just 3
    y <- Just "!"
    Just (show x ++ y)

Puede parecer que hemos ganado la habilidad de cosas de valores Maybe sin tener que preocuparnos por comprobar en cada paso si dichos valores son valores Just o valores Nothing ¡Genial! Si alguno de los valores que intentamos extraer es Nothing, la expresión do entera se reducirá a Nothing. Estamos extrayendo sus (probablemente existentes) valores y dejamos a >>= que se preocupe por el contexto de dichos valores. Es importante recordar que la notación do es solo una sintaxis diferente para encanedar valores monádicos.

En una expresión do cada línea es un valor monádico. Para inspecionar el resultado de una línea utilizamos <-. Si tenemos un Maybe String y le damos una variable utilizando <-, esa variable será del tipo String, del mismo modo que cuando utilizábamos >>= para pasar valores monádicos a las funciones lambda. El último valor monádico de una expresión, en este caso Just (show x ++ y), no se puede utilizar junto a <- porque no tendría mucho sentido traducimos de nuevo la expresión do a una ecandención de aplicaciones >>=. Esta última línea será el resultado de unir toda la expresión do en un único valor monádico, teniendo en cuenta el hecho de que puede ocurrir un fallo en cualquiera de los pasos anteriores.

Por ejemplo:

ghci> Just 9 >>= (\x -> Just (x > 8))
Just True

Como el parámetro a la izquierda de >>= es un valor Just, la función lambda es aplicada a 9 y el resultado es Just True. Si reescribimos esto en notación do obtenemos:

marySue :: Maybe Bool
marySue = do
    x <- Just 9
    Just (x > 8)

Si comparamos ambas es fácil deducir porque el resultado de toda la expresión do es el último valor monádico.

La función routine que escribimos anteriormente también puede ser escrita con una expresión do. landLeft y landRight toman el número de pájaros y la barra para producir una nueva barra dentro de un valor Just, a no ser que nuestro funambulista se caiga y produzca Nothing. Utilizamos >>= porque cada uno de los pasos depende del anterior y cada uno de ellos tiene el contexto de un posible fallo. Aquí tienes dos pájaros posandose en lado izquierdo, luego otros dos pájaros posandose en lado derecho y luego otro más aterrizando en la izquierda:

routine :: Maybe Pole
routine = do
    start <- return (0,0)
    first <- landLeft 2 start
    second <- landRight 2 first
    landLeft 1 second

Vamos a ver si funciona:

ghci> routine
Just (3,2)

¡Lo hace! ¡Genial! Cuando creamos esta función utilizando >>=, utilizábamos cosas como return (0,0) >>= landLeft 2, porque landLeft 2 es una función que devuelve un valor del tipo Maybe. Sin embargo con las expresiones do, cada línea debe representar un valor monádico. Así que tenemos que pasar explícitamente cada Pole anterior a las funciones landLeft y landRight. Si examinamos las variables a las que ligamos los valores Maybe, start sería (0,0), first sería (2,0) y así sucesivamente.

Debido a que las expresiones do se escriben línea a línea, a mucha gente le puede parecer código imperativo. Pero lo cierto es que son solo secuenciales, de forma que cada línea depende del resultado de las líneas anteriores, junto con sus contextos (en este caso, dependen de si las anterioeres fallan o no).

De nuevo, vamos a volver a ver como sería este código si no tuvieramos en cuenta los aspectos monádicos de Maybe:

routine :: Maybe Pole
routine =
    case Just (0,0) of
        Nothing -> Nothing
        Just start -> case landLeft 2 start of
            Nothing -> Nothing
            Just first -> case landRight 2 first of
                Nothing -> Nothing
                Just second -> landLeft 1 second

Fíjate como en caso de no fallar, la tupla dentro de Just (0,0) se convierte en start, el resultado de landLeft 2 start se convierte en first, etc.

Si queremos lanzar a Pierre una piel de plátano en notación do solo tenemos que hacer lo siguiente:

routine :: Maybe Pole
routine = do
    start <- return (0,0)
    first <- landLeft 2 start
    Nothing
    second <- landRight 2 first
    landLeft 1 second

Cuando escribirmos una línea en la notación do sin ligar el valor monádico con <-, es como poner >> después de ese valor monádico cuyo reulstado queremos que ignore. Secuenciamos el valor monádico pero ignoramos su resultado ya que no nos importa y es más cómodo que escribir _ <- Nothing, que por cierto, es lo mismo.

Cuando utilizar la notación do y cuando utilizar >>= depende de ti. Creo que este ejemplo se expresa mejor escribiendo explícitamente los >>= ya que cada paso depende específicamente del anterior. Con la notación do tenemos que especificar en que barra van a aterrizar los pájaros incluso aunque siempre aterrizen en la barra anterior.

En la notación do, cuando ligamos valore monádicos a variables, podemos utilizar ajustes de patrones de la misma forma que los usábamos con las expresiones let o con los parámetros de las funciones. Aquí tienes un ejemplo de uso de ajuste de patrones dentro de una expresión do:

justH :: Maybe Char
justH = do
    (x:xs) <- Just "hello"
    return x

Hemos ajustado un patrón para obtener el primer carácter de la cadena "hello" y luego lo devolvemos como resultado. Así que JustH se evalua a Just 'h'.

¿Qué pasaria si este ajuste fallara? Cuando un ajuste de patrones falla en una función se utiliza el siguiente ajuste. Si el ajuste falla en todos los patrones de una función, se lanza un error y el programa podría terminar. Por otra parte si el ajuste falla en una expresión let, se lanza un error directamente ya que no existe ningún mecanismo que no lleve a otro patrón que ajustar. Cuando un ajuste falla dentro de una expresión do se llama a la función fail. Ésta es parte de la clase de tipos Monad y nos permite ver este fallo como un fallo en el contexto del valor monádico en lugar de hacer que el programa termine. Su implementación por defecto es:

fail :: (Monad m) => String -> m a
fail msg = error msg

Así que por defecto hace que el programa termine, pero las mónadas que incorporan un contexto para un posible fallo (como Maybe) normalmente implementan el suyo propio. En Maybe se implementa así:

fail _ = Nothing

Ignora el mensaje de error y devuelve Nothing. Así que cuando un ajuste falla dentro de un valor Maybe que utiliza una expresión do, el valor entero se reduce a Nothing. Suele ser preferiable a que el programa termine. Aquí tienes una expresión do con un patrón que no se ajustará y por tanto fallará:

wopwop :: Maybe Char
wopwop = do
    (x:xs) <- Just ""
    return x

El ajuste falla, así que sería igual a remplazar toda la línea por Nothing. Vamos a probarlo:

ghci> wopwop
Nothing

Este fallo en el ajuste de un patrón genera un fallo en el contexto de nuestra mónada en lugar de generar un fallo en el programa, lo cual es muy elegante.

La mónada lista

Hasta ahora hemos visto como los valores del tipo Maybe pueden verse como valores en un contexto de un posible fallo y que podemos incorportar el tratamiento de estos posibles fallos utilizando >>= para pasar los parámetros a las funciones. En esta sección vamos a echar un vistazo a como podemos utilizar los aspectos monádicos de las listas llevanso así el no determinsmo a nuestro código de forma legible.

Ya hemos hablado de como las listas representan valores no deterministas cuando se utilizan como funtores aplicativos. Un valor como 5 es determinista. Tiene un único valor y sabemos exactamente cual es. Por otra parte, un valor como [3,8,9] consiste en varios resultados, así que lo podemos ver como un valor que en realidad es varios valores al mismo tiempo.

Al utilizar las listas como funtores aplicativos vemos fácilmente este no determinismo:

ghci> (*) <$> [1,2,3] <*> [10,100,1000]
[10,100,1000,20,200,2000,30,300,3000]

Todas la posibles soluciones de multiplicar los elementos de la izquierda por los elementos de la derecha aparecen en la lista resultado. Cuando trabajamos con el no determinismo, exsiten varias opciones que podemos tomar, así que básicamente probamos todas ellas y por lo tanto el resultado también otro valor no determinista, solo que con unos cuantos valores más.

Este contexto de no determinismo se translada a las mónadas fácilmente. Vamos a ver como luce la instancia de Monad para las listas:

instance Monad [] where
    return x = [x]
    xs >>= f = concat (map f xs)
    fail _ = []

return es lo mismo que pure, así que ya estamos familiarizados con ella. Toma un valor y lo introducie en el mínimo contexto por defecto que es capaz de albergar ese valor. En otras palabras, crea una lista que contiene como único elemento dicho valor. Resulta útil cuando necesitmos que un valor determinista interactue con otros valores no deterministas.

Para entender mejor como funciona >>= con las listas veremos un ejemplo de su uso. >>= toma un valor con un contexto (un valor monádico) y se lo pasa a una función que toma valores normales y devuelve otro valor en el mismo contexto. Si esta función devolviera un valor normal en luegar de un valor monádico, >>= no sería muy útil ya que depués de usarlo perderíamos el contexto. De cualquier modo, vamos vamos a intentar pasar un valor no determinista a una función:

ghci> [3,4,5] >>= \x -> [x,-x]
[3,-3,4,-4,5,-5]

Cuando utilizamos >>= con Maybe, el valor monádico se pasaba a la función teniendo en cuenta la existencia de un posible fallo. Aquí >>= se preocupa del no determinismo por nosotros. [3,4,5] es un valor no determinista y se lo hemos pasado a otra función que devuelve valores no deterministas también. El resultado final también es no determinista y contiene los posibles resultados de aplicar la función \x -> [x,-x] a todos los elementos de [3,4,5]. Esta función toma un número y produce dos resultados: uno negado y otro igual que el original. De esta forma cuando utilizamos >>= para pasar la lista a esta función todos los números son negados pero también se mantienen los originales. La x de la función lambda toma todos los posibles valores de la lista que pasamos como parámetro.

Para ver como se consigue este resultado solo tenemos que ver la implementación. Primero, empezamos con la list [3,4,5]. Luego mapeamos la función lambda sobre ella y obtenemos el siguiente resultado:

[[3,-3],[4,-4],[5,-5]]

La función lambda se aplica a cada elemento por lo que obtenemos una lista de listas. Para terminar simplemente concatenamos las listas y punto final ¡Acabamos de aplicar un función no determinista a una valor no determinista!

El no determinismo también soporta la existencia de fallos. La lista vacía [] es muy parecido a Nothing ya que ambos representan la ausencia de un resultado. Por este motivo la función fail se define simplemente con la lista vacía. El mensaje de error se ignora.

ghci> [] >>= \x -> ["bad","mad","rad"]
[]
ghci> [1,2,3] >>= \_ -> []
[]

En la primera línea se pasa una lista vacía a la función lambda. Como la lista no tienen ningún elemento, no podemos pasar nada a la función así que el resultado final es también la lista vacía. Es similiar a pasar Nothing a una función. En la segunda línea, cada elemento de la lista se pasa a la función, pero estos elementos son ignorados y la función simplemente devuelve una lista vacía. Como la función falla para todos los elementos de la lista, el resultado final es la lista vacía.

Del mismo modo que pasaba con los valores del tipo Maybe, podemos concatenar varios >>= propagando así el no deterministmo:

ghci> [1,2] >>= \n -> ['a','b'] >>= \ch -> return (n,ch)
[(1,'a'),(1,'b'),(2,'a'),(2,'b')]

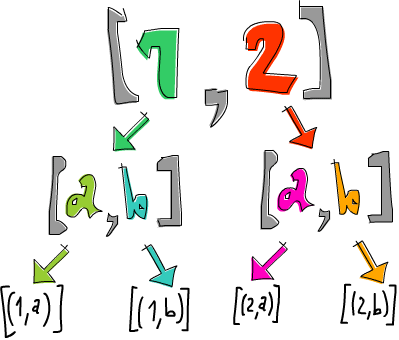
Los elemenots de lista [1,2] se ligan a n y los elementos de ['a','b'] se ligan a ch. Luego, hacemos return (n,ch) (o [(n,ch)]), lo que significa que tomamos una dupla (n,ch) y la introducimos en el contexto mínimo por defecto. En este caso, se crea la lista más pequeña posible que pueda albergar (n,ch) como resultado de forma que posea tan poco no determinismo como sea posible. Dicho de otro modo, el efecto del contexto es mínimo. Lo que estamos implementando es: para cada elemento en [1,2] y para cada elemento de ['a','b'] producimos una dupla para combinación posible.

En términos generales, como return lo único que hace es introducir un valor en el contexto mínimo, no posee ningún efecto extra (como devolver un fallo en Maybe o devolver en un valor aún menos determinista en caso de las listas) sino que sólamete toma un valor como resultado.

Nota

Cuando tenemos varios valores no deterministas interactuando, podemos ver su cómputo como un árbol donde cada posible resultado representa una rama del árbol.

Aquí tienes la expresión anterior escrita con notación do:

listOfTuples :: [(Int,Char)]
listOfTuples = do
    n <- [1,2]
    ch <- ['a','b']
    return (n,ch)

Así parece más obvio que n toma cada posible valor de [1,2] y que ch toma cada posible valor de ['a','b']. Del mismo modo que con Maybe, estamos extrayendo valores normales de un valor monádico y dejamos que >>= se preocupe por el contexto. El contexto en este caso es el no determinismo.

Cuando vemos las listas utilizando la notación do puede que nos recuerde a algo que ya hemos visto. Mira esto:

ghci> [ (n,ch) | n <- [1,2], ch <- ['a','b'] ]
[(1,'a'),(1,'b'),(2,'a'),(2,'b')]

¡Sí! ¡Listas por comprensión! Cuando utilizábamos la notación do, n tomaba cada posible elemento de [1,2] y ch tomaba cada posible elemento de ['a','b'] y luego introducíamos (n,ch) en el contexto por defecto (una lista unitaria) para devolverlo como resultado final sin tener que introducir ningún tipo de no determinismo adicional. En esta lista por comprensión hacemos exactamente lo mismo, solo que no tenemos que escribir return al final para dar como resultado (n,ch) ya que la lista por comprensión se encarga de hacerlo.

De hecho, las listas por comprensión no son más que una alternativa sintáctica al uso de listas como mónadas. Al final, tanto las listas por comprensión como la notación do se traduce a una concatenación de >>= que representan el no determinismo.

Las listas por comprensión nos perminten filtrar la lista. Por ejemplo, podemos filtrar una lista de número para quedarnos únicamente con los números que contengan el dígito 7:

ghci> [ x | x <- [1..50], '7' `elem` show x ]
[7,17,27,37,47]

Aplicamos show a x para convertir el número en una cadena y luego comprobamos si el carácter '7' froma parte de en esa cadena. Muy ingenioso. Para comprender como se traduce estos filtros de las listas por comprensión a la mónada lista tenemos que ver la función guard y la clase de tipos MonadPlus. La clase de tipos MonadPlus representa mónadas que son también monoides. Aquí tienes la definición:

class Monad m => MonadPlus m where
    mzero :: m a
    mplus :: m a -> m a -> m a

mzero es un sinónimo del mempty que nos encontramos en la clase Monoid y mplus correponde con mappend. Como las listas también son monoides a la vez que mónadas podemos crear una isntancia para esta clase de tipos:

instance MonadPlus [] where
    mzero = []
    mplus = (++)

Para las listas mzero representa un cómputo no determinista que no devuelve ningún resultado, es decir un cómputo que falla. mplus une dos valores no deterministas en uno. La función guard se define así:

guard :: (MonadPlus m) => Bool -> m ()
guard True = return ()
guard False = mzero

Toma un valor booleano y si es True, introduce () en el mínimo contexto por defecto. En caso contrario devuleve un valor monádico que representa un fallo. Aquí la tienes en acción:

ghci> guard (5 > 2) :: Maybe ()
Just ()
ghci> guard (1 > 2) :: Maybe ()
Nothing
ghci> guard (5 > 2) :: [()]
[()]
ghci> guard (1 > 2) :: [()]
[]

Parece interesante pero, ¿es útil? En la mónada lista utilizamos esta función para filtrar una series de cómputos no deterministas. Observa:

ghci> [1..50] >>= (\x -> guard ('7' `elem` show x) >> return x)
[7,17,27,37,47]

El resultado es el mismo que la lista por comprensión anterior. ¿Cómo consigue guard este resultado? Primero vamos a ver se utiliza guard junto a >>:

ghci> guard (5 > 2) >> return "cool" :: [String]
["cool"]
ghci> guard (1 > 2) >> return "cool" :: [String]
[]

Si el predicado de guard se satisface, el resultado es una lista con una tupla vacía. Luego utilizamos >> para ignorar esta tupla vacía y devolver otra cosa como resultado. Sin embargo, si guard falla, no alcanzaremos el return ya que si pasamos una lista vacía a una funcón con >>= el resultado siempre será una lista vacía. guard simplemente dice: si el predicado es False entonces devolvemos un fallo, en caso contrario devolvemos un valor que contiene un resultado ficticio (). Esto permite que el encadenamiento continue.

Así sería el ejemplo anterior utilizando la notación do:

sevensOnly :: [Int]
sevensOnly = do
    x <- [1..50]
    guard ('7' `elem` show x)
    return x

Si hubiéramos olvidado devolver x como resultado final con return, la lista resultante sería una lista de tuplas vacías en lugar de una lista de enteros. Aquí tienes de nuevo la lista por comprensión para que compares:

ghci> [ x | x <- [1..50], '7' `elem` show x ]
[7,17,27,37,47]

Filtrar una lista por comprensión es igual que usar guard.

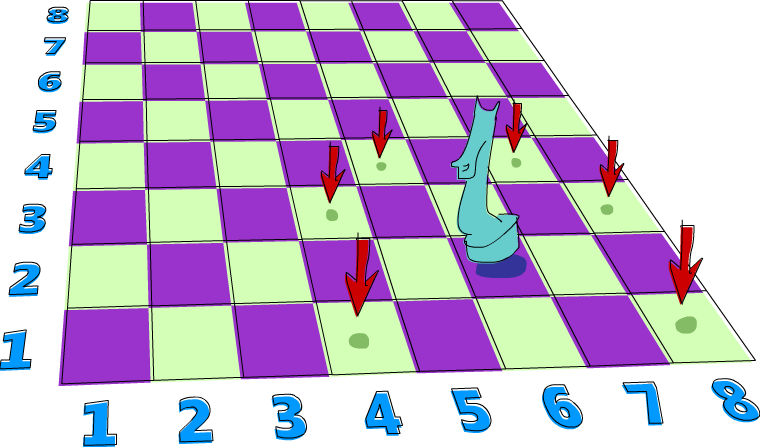
El salto del caballo

Vamos a ver un problema que tiende a resolverse utilizando no determinismo. Digamos que tenemos un tablero de ajedrez y como única pieza un caballo. Queremos saber si el caballo peude alcanzar una determinada posición en tres movimientos. Utilizaremos una dupla de números para representar la posición del caballo en el tablero. El primer número representará la columna en la que está el caballo y el segundo representará la fila.

Vamos a crear un sinónimo de tipo para representar la posición actual del caballo:

type KnightPos = (Int,Int)

Digamos que el caballo empieza en (6,2) ¿Puede alcanzar (6,1) en solo tres movimientos? Vamos a ver. Si empezamos en (6,2), ¿cuál sería el mejor movimiento a realizar? Ya se, ¡Todos! Tenemos el no determinismo a nuestra disposición, así que en lugar de decidirnos por un movimiento, hagámoslos todos. Aquí tienes una función que toma la posición del caballo y devuelve todos las posibles posiciones en las que se encontrará depués de moverse.

moveKnight :: KnightPos -> [KnightPos]
moveKnight (c,r) = do
    (c',r') <- [(c+2,r-1),(c+2,r+1),(c-2,r-1),(c-2,r+1)
               ,(c+1,r-2),(c+1,r+2),(c-1,r-2),(c-1,r+2)
               ]
    guard (c' `elem` [1..8] && r' `elem` [1..8])
    return (c',r')

El caballo puede tomar un paso en horizontal o vertical y otros dos pasos en horizontal o vertical pero siempre haciendo un movimiento horizontal y otro vertical. (c',r') toma todos los valores de los elementos de la lista y luego guard se encarga de comprobar que la nueva posicion permanece dentro del tablero. Si no lo está, produce una lista vacía y por lo tanto no se alcanza return (c',r') para esa posición.

También se puede escribir esta función sin hacer uso de la mónada lista, aunque lo acabamos de hacer solo por diversión. Aquí tienes la misma función utilizando filter:

moveKnight :: KnightPos -> [KnightPos]
moveKnight (c,r) = filter onBoard
    [(c+2,r-1),(c+2,r+1),(c-2,r-1),(c-2,r+1)
    ,(c+1,r-2),(c+1,r+2),(c-1,r-2),(c-1,r+2)
    ]
    where onBoard (c,r) = c `elem` [1..8] && r `elem` [1..8]

Ambas son iguales, así que elige la que creas mejor. Vamos a probarla:

ghci> moveKnight (6,2)
[(8,1),(8,3),(4,1),(4,3),(7,4),(5,4)]
ghci> moveKnight (8,1)
[(6,2),(7,3)]

¡Funciona perfectamente! Toma una posición y devuelve todas las siguientes posiciones de golpe. Así que ahora que tenemos la siguiente posición de forma no determinista, solo tenemos que aplicar >>= para pasársela a moveKnight. Aquí tienes una función que toma una posición y devuelve todas las posiciones que se pueden alcanzar en tres movimientos:

in3 :: KnightPos -> [KnightPos]
in3 start = do
    first <- moveKnight start
    second <- moveKnight first
    moveKnight second

Si le pasamos (6,2), el resultado será un poco grande porque si existe varias formas de llegar a la misma posición en tres movimientos, tendremos varios elementos repetidos. A continuación sin usar la notación do:

in3 start = return start >>= moveKnight >>= moveKnight >>= moveKnight

Al utiliza >>= obtenemos todos los posibles movimientos desde el inicio y luego cuando utilizamos >>= por segunda vez, para cada posible primer movimiento calculamos cada posible siguiente movimiento. Lo mismo sucede para el tercer movimiento.

Introducir un valor en el contexto por defecto utilizando return para luego pasarlo como parámetro utilizando >>= es lo mismo que aplicar normalemente la función a dicho valor, aunque aquí lo hemos hecho de todas formas.

Ahora vamos a crear una función que tome dos posiciones y nos diga si la última posición puede ser alcanzada con exáctamente tres pasos:

canReachIn3 :: KnightPos -> KnightPos -> Bool
canReachIn3 start end = end `elem` in3 start

Generamos todas las posibles soluciones que se pueden generar con tres pasos y luego comprobamos si la posición destino se encuentra dentro de estas posibles soluciones. Vamos a ver si podemos alcanzar (6,1) desde (6,2) en tres movimientos:

ghci> (6,2) `canReachIn3` (6,1)
True

¡Sí! ¿Y de (6,2) a (7,3)?

ghci> (6,2) `canReachIn3` (7,3)
False

¡No! Como ejercicio, puedes intentar modificar esta función para que cuando se pueda alcanzar esta posición te diga que pasos debes seguir. Luego, veremos como modificar esta función de forma que también pasemos como parámetro el número de pasos.

Las leyes de las mónadas

De la misma forma que lo funtores aplicativos, a la vez que lo funtores normales, las mónadas vienen con una serie de leyes que todas las mónadas que se precien deben cumplir. Solo porque algo tenga una instancia de la clase Monad no significa que sea una mónada, solo significa que ese algo tiene una instancia para la clase Monad. Para que un tipo sea realmente una mónada debe satisfacer las leyes. Estas leyes nos permiten asumir muchas cosas acerca del comportamiento del tipo.

Haskell permite que cualquier tipo tenga una instancia de cualquier clase de tipos siempre que los tipos concuerden. No puede comprobar si las leyes de las mónadas se cumplen o no, así que si estamos creando una instancia para la clase Monad, tenemos que estar lo suficientemente seguros de que la mónada satisface las leyes para ese tipo. Los estar seguros de que los tipos que vienen en la biblioteca estándar cumplen estas leyes, pero luego, cuando creemos nuestras própias mónadas, tendremos que comprobar manualmente si se cumplen las leyes o no. No te asuste, no son complicadas.

Identidad por la izquierda

La primera ley establece que tomamos un valor, lo introducimos en el contexto por defecto utilizando return y luego pasamos el resultado a una función utilizando >>=, el resultado debe ser igual que aplicar la función directamente a ese valor. Informalmente:

• return x >>= f es exactamente lo mismo que f x.

Si vemos los valores monádicos como valores con un cierto contexto y return toma un valor y lo introduce en el contexto mínimo por defecto que puede albergar ese valor, tiene sentido que, como ese contexto en realidad es mínimo, al pasar el valor monádico a una función no debe haber mucha diferencia con aplicar la función a un valor normal, y de hecho, es exactamente lo mismo.

Para la mónada Maybe, return se define como Just. La mónada Maybe trata acerca de posibles fallos, así que si tenemos un valor y lo introducimos en dicho contexto, tiene sentido tratar este valor como cómputo correcto, ya que, bueno, sabemos cual es ese valor. Aquí tienes un par de usos de return:

ghci> return 3 >>= (\x -> Just (x+100000))
Just 100003
ghci> (\x -> Just (x+100000)) 3
Just 100003

En cambio para la mónada lista, return intruce un valor en una lista unitaria. La implementación de >>= para las listas recorre todos los elementos de la lista y les aplica una función, pero como solo hay un elemento en la lista, es lo mismo que aplicar la función a ese valor:

ghci> return "WoM" >>= (\x -> [x,x,x])
["WoM","WoM","WoM"]
ghci> (\x -> [x,x,x]) "WoM"
["WoM","WoM","WoM"]

Dijimos que para la mónada IO, return simplemente creaba una acción que no tenia ningún efecto secundario y solo albergaba el valor que pasábamos como parámetro. Así que también cumple esta ley.

Identidad por la derecha

La segunda ley establece que si tenemos un valor monádico y utilizamos >>= para pasarselo a return, el resultado debe ser el valor monádico original. Formalemente:

• m >>= return es igual que m.

Esta ley puede parecer un poco menos obvia que la primera, pero vamos a echar un vistazo para ver porque se debe cumplir. Pasamos valores monádicos a las funciones utilizando >>=. Estas funciones toman valores normales y devuelven valores monádicos. return es una también es una de estas funciones. Como ya sabemos, return introduce un valor en el contexto mínimo que pueda albergar dicho valor. Esto quiere decir que, por ejemplo para Maybe, no introduce ningún fallo; para las listas, no introduce ningún no determinismo adicional. Aqui tienes una prueba con algunas mónadas:

ghci> Just "move on up" >>= (\x -> return x)
Just "move on up"
ghci> [1,2,3,4] >>= (\x -> return x)
[1,2,3,4]
ghci> putStrLn "Wah!" >>= (\x -> return x)
Wah!

Si echamos un vistazo más de cerca al ejemplo de las listas, la implementación de >>= para las listas es:

xs >>= f = concat (map f xs)

Así que cuando pasamos [1,2,3,4] a return, primero return se mapea sobre [1,2,3,4], devolviendo [[1],[2],[3],[4]] y luego se concatena esta lista obteniendo así la original.

La identida por la izquierda y la identadad por la derecha son leyes que establecen el comportamiento de return. Es una función importante para convertir valores normales en valores monádicos y no sería tan útil si el valor monádico que produciera hicera mucha más cosas.

Asociatividad

La última ley de las mónadas dice que cuando tenemos una cadena de aplicaciones funciones monádicas con >>=, no importa el orden en el que estén anidadas. Escrito formalmente:

• (m >>= f) >>= g es igual a >>= (x -> f x >>= g).

Mmm... ¿Qué esta pasando aquí? Tenemos un valor monádico, m y dos funciones monádica f y g. Hacemos (m >>= f) >>= g, es decir, pasamos m a f, lo cual devuelve un valor monádico. Luego pasamos ese valor monádico a g. En la expresión m >>= (\x -> f x >>= g) tomamos un valor monádico y se lo pasamos a una función que pasa el resultado de f x a g. Quizá no es fácil ver como ambas expresiones son iguales, así que vamos a ver un ejemplo para aclarár las dudas.

¿Recuerdas cuando el funambulista Pierra caminaba sobre una cuerda con ayuda de una barra de equilibrio? Para simular el aterrizaje de los pájaros sobre esta barra de equilibrio utilizábamos una cadena de funciones que podían fallar:

ghci> return (0,0) >>= landRight 2 >>= landLeft 2 >>= landRight 2
Just (2,4)

Empezábamos con Just (0,0) y luego pasábamos este valor a la siguiente función monádica, landRight 2. El resultado de ésta era otro valor monádico que pasábamos a la siguiente función de la cadena y así sucesivamente. Si mostramos la asociatividad de forma explícita, la expresión quedaría así:

ghci> ((return (0,0) >>= landRight 2) >>= landLeft 2) >>= landRight 2
Just (2,4)

Pero también podemos esxpresarlo así:

return (0,0) >>= (\x ->
landRight 2 x >>= (\y ->
landLeft 2 y >>= (\z ->
landRight 2 z)))

return (0,0) es lo mismo que Just (0,0) y cuando se lo pasamos a la función lambda, x se convierte en (0,0). landRight toma un número de pájaros y una barra (una dupla de números) y eso es lo que le pasamos. Devuelve Just (0,2) y cuando se lo pasamos a la siguiente función lambda, y es (0,2). Continua hasta el último aterrizaje de pájaros que produce Just (2,4), que de hecho es el resultado final de la expresión.

Resumiendo, no importa como anides el paso de valores monádicos, lo que importa es su significado. Otra forma de ver esta ley sería: consideremos la composición de dos funciones, f y g. La composición de funciones se implementa como:

(.) :: (b -> c) -> (a -> b) -> (a -> c)
f . g = (\x -> f (g x))

El tipo de g es a -> b y el de f es b -> c, y las unimos en una nueva función con tipo a -> c cuyo parámetro será pasado entre las funciones anteriores. Y ahora, ¿qué pasaria si estas dos funciones fueran monádicas? es decir ¿qué pasaria si estas funciones devolvieran valores monádicos? Si tuvieramos una función del tipo a -> m b, no podríamos pasar su resultado directamente a una función del tipo b -> m c, ya que esta función solo acepta valores normales y no monádicos. Sin embargo podemos utilizar >>= para poder permitirlo. Así que si utilizamos >>=, podemos definir la composición de dos funciones monádicas como:

(<=<) :: (Monad m) => (b -> m c) -> (a -> m b) -> (a -> m c)
f <=< g = (\x -> g x >>= f)

Ahora podemos componer nuevas funciones monádicas a partir de otras:

ghci> let f x = [x,-x]
ghci> let g x = [x*3,x*2]
ghci> let h = f <=< g
ghci> h 3
[9,-9,6,-6]

Genial ¿Y qué tiene que ver esto con la ley de asociatividad? Bueno, cuando vemos la ley como una ley de composiciones, ésta dice que f <=< (g <=< h) debe ser igual a (f <=< g) <=< h. Es otra forma de decir que para las mónadas, no importa el orden del anidamiento.

Si traducimos las dos primeras leyes para que utilicen <=<, entonces, la primera ley dice que para cada función monádica f, f <=< return es lo mismo que f y la ley de identidad por la derecha dice que return <=< f es también igual a f.

Es parecido a lo que ocurre con las funciones normales, (f . g) . h es lo mismo que f . (g . h), f . id es igual a f y id . f es también igual a f.

En este capítulo hemos visto las bases de la mónadas y hemos aprendido a utilizar las mónadas Maybe y las listas. En el siguiente capítulo, echaremos un vistazo a un puñado más de mónadas y también aprenderemos como crear nuestras propias mónadas.