Resolviendo problemas de forma funcional¶

En este capítulo, veremos un par de problemas interesantes y como resolverlos de forma funcional y elegante. Probablemente no introduciremos ningún concepto nuevo, solo vamos a practicar nuestras habilidades de programación y calentar un poco. Cada sección presentará un problema diferente. Primero describiremos el problema, luego intentaremos resolverlo y trataremos de encontrar la mejor (o al menos no la peor) forma de resolverlo.

Notación polaca inversa¶

Normalmente cuando escribíamos expresiones matemáticas en la escuela lo hacíamos de forma infija. Por ejemplo, 10 - (4 + 3) * 2. +, * y - son operadores infijos, al igual que los funciones infijas que conocemos de Haskell (+, elem, etc.). Resulta bastante útil, ya que nosotros, como humanos, podemos analizar fácilmente estas expresiones. La pega es que tenemos que utilizar paréntesis para especificar la precedencia.

La Notación polaca inversa es otra forma de escribir expresiones matemáticas. Al principio parece un poco enrevesado, pero en realidad es bastante fácil de entender y utilizar ya que no hay necesidad de utilizar paréntesis y muy fácil de utilizar en la calculadoras. Aunque las calculadoras más modernas usan una notación infija, todavía hay gente que lleva calculadoras RPN (del inglés, Reverse Polish Notation). Así se vería la expresión infija anterior en RPN: 10 4 3 + 2 * - ¿Cómo calculamos el resultado de esto? Bueno, piensa en una pila. Recorremos la expresión de izquierda a derecha. Cada vez que encontramos un número, lo apilamos. Cuando encontramos un operador, retiramos los dos números que hay en la cima de la pila, utilizamos el operador con ellos y apilamos el resultado de nuevo. Cuando alcancemos el final de la expresión, debemos tener un solo número en la pila si la expresión estaba bien formada, y éste representa el resultado de la expresión

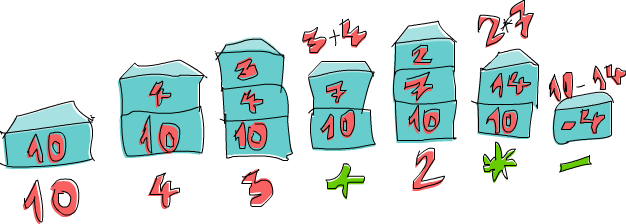
¡Vamos a realizar la operación 10 4 3 + 2 * - juntos! Primero apilamos 10 de forma que ahora nuestra pila contiene un 10. El siguiente elemento es un 4, así que lo apilamos también. La pila ahora contiene 10, 4. Hacemos los mismo para el 3 y conseguimos una pila que contiene 10, 4, 3. Ahora, encontramos un operador, +. Retiramos los dos números que se encuentran en la cima de la pila (de forma que la pila se quedaría de nuevo solo con 10), sumamos esos dos números y apilamos el resultado. La pila contiene 10, 7 ahora mismo. Apilamos 2 y obtenemos 10, 7, 2. Multiplicamos 7 y 2 y obtenemos 14, así que lo apilamos y la pila ahora contendrá 10, 14. Para terminar hay un -. Retiramos 10 y 14 de la pila, restamos 14 a 10 y apilamos el resultado. El número que contiene la pila es -4 y como no hay más números ni operadores en la expresión, ese es el resultado.

Ahora que ya sabemos como calcular una expresión RPN a mano, vamos a pensar en como podríamos hacer que una función Haskell tomara como parámetro una cadena que contenga una expresión RPN, como 10 4 3 + 2 * -, y nos devolviera el resultado.

¿Cuál sería el tipo que debería tener esta función? Queremos que tome una cadena y produzca un número como resultado. Así que lo más seguro es que el tipo sea algo como solveRPN :: (Num a) => String -> a.

Nota

Ayuda mucho pensar primero en cual será la declaración de tipo de una función antes de preocuparnos en como implementarla para luego escribirla. Gracias al sistema de tipos de Haskell, la declaración de tipo de una función nos da mucha información acerca de ésta.

Bien. Cuando implementemos la solución de un problema en Haskell, a veces es bueno volver a ver como lo solucionamos a mano para ver si podemos sacar algo que nos ayude. En este caso vimos que tratábamos cada número u operador que estaba separado por un espacio como un solo elemento. Así que podría ayudarnos si empezamos rompiendo una cadena como "10 4 3 + 2 * -" en una lista de elementos como ["10","4","3","+","2","*","-"].

A continuación ¿Qué fue lo siguiente que hicimos mentalmente? Recorrimos la expresión de izquierda a derecha mientras manteníamos una pila ¿Te recuerda la frase anterior a algo? Recuerda la sección que hablaba de los pliegues, dijimos que cualquier función que recorra una lista de izquierda a derecha, elemento a elemento, y genere (o acumule) un resultado (ya sea un número, una lista, una pila o lo que sea) puede ser implementado con un pliegue.

En este caso, vamos a utilizar un pliegue por la izquierda, ya que vamos a recorrer la lista de izquierda a derecha. Nuestro acumulador será la pila, y por la tanto el resultado será también una pila, solo que, como ya hemos visto, contendrá un solo elemento.

Una cosa más que tenemos que pensar es, bueno ¿Cómo vamos a representar la pila? Propongo que utilicemos una lista. También propongo que mantengamos en la cabeza de la lista la cima de la pila. De esta forma añadir un elemento en la cabeza de la lista es mucho más eficiente que añadirlo al final. Así que si tenemos una pila como, 10, 4, 3, la representaremos con una lista como [3,4,10].

Ahora tenemos suficiente información para bosquejar vagamente nuestra función. Tomará una cadena como "10 4 3 + 2 * -" y la romperá en una lista de elementos utilizando words de forma que obtenga ["10","4","3","+","2","*","-"]. Luego, utilizará un pliegue por la izquierda sobre esa lista y generará una pila con un único elemento, como [-4]. Tomará ese único elemento de la lista y ese será nuestro resultado final.

Aquí tienes el esqueleto de esta función:

import Data.List

solveRPN :: (Num a) => String -> a
solveRPN expression = head (foldl foldingFunction [] (words expression))
    where   foldingFunction stack item = ...

Tomamos una expresión y la convertimos en una lista de elementos. Luego plegamos una función sobre esta lista. Ten en cuenta que [] representa es acumulador inicial. Dicho acumulador es nuestra pila, así que [] representa la pila vacía con la que comenzamos. Luego de obtener la pila final que contiene un único elemento, llamamos a head sobre esa lista para extraer el elemento y aplicamos read.

Solo nos queda implementar la función de pliegue que tomará una pila, como [4,10] y un elemento, como "3" y devolverá una nueva pila [4,10,3]. Si la pila es [4,10] y el elemento es "*", entonces tenemos que devolver [40]. Pero antes, vamos a transformar nuestra función al estilo libre de puntos ya que tiene muchos paréntesis y me está dando grima.

import Data.List

solveRPN :: (Num a) => String -> a
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction stack item = ...

Ahí lo tienes. Mucho mejor. Como vemos, la función de pliegue tomará una pila y un elemento y devolverá una nueva pila. Utilizaremos ajuste de patrones para obtener los elementos de la cima de la pila y para obtener los operadores, como "*" o "-".

solveRPN :: (Num a, Read a) => String -> a
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction (x:y:ys) "*" = (x * y):ys
            foldingFunction (x:y:ys) "+" = (x + y):ys
            foldingFunction (x:y:ys) "-" = (y - x):ys
            foldingFunction xs numberString = read numberString:xs

Hemos utilizado cuatro patrones. Los patrones se ajustarán de arriba a abajo. Primero, la función de pliegue verá si el elemento actual es "*". Si lo es, tomará una lista como podría ser [3,4,9,3] y llamará a sus dos primeros elementos x e y respectivamente. En este caso, x``sería ``3 e y sería 4. ys sería [9,3]. Devolverá una lista como ys, solo que tendrá x por y como cabeza. Con esto retiramos los dos elementos superiores de la pila, los multiplicamos y apilamos el resultado de nuevo en la pila. Si el elemento no es "*", el ajuste de patrones fallará y continuará con "+", y así sucesivamente.

Si el elemento no es ninguno de los operadores, asumimos que es una cadena que representa un número. Simplemente llamamos a read sobre esa esa cadena para obtener el número y devolver la misma pila pero con este número en la cima.

¡Y eso es todo! Fíjate que hemos añadido una restricción de clase extra (read a) en la declaración de la función, ya que llamamos a read sobre la cadena para obtener un número. De esta forma la declaración dice que puede devolver cualquier tipo que forme parte de las clases de tipos Num y Read (como Int, Float, etc.).

Para la lista de elementos ["2", "3", "+"], nuestra función empezará plegando la lista desde la izquierda. La pila inicial será []. Llamará a la función de pliegue con [] como pila (acumulador) y "2" como elemento. Como dicho elemento no es un operador, utilizará read y añadirá el número al inicio de []. Así que ahora la pila es [2] y la función de pliegue será llamada con [2] como pila y "3" como elemento, produciendo una nueva pila [3,2]. Luego, será llamada por tercera vez con [3,2] como pila y con "+" como elemento. Esto hará que los dos números sean retirados de la pila, se sumen, y que el resultado sea apilado de nuevo. La pila final es [5], que contiene el número que devolveremos.

Vamos a jugar con esta función:

ghci> solveRPN "10 4 3 + 2 * -"
-4
ghci> solveRPN "2 3 +"
5
ghci> solveRPN "90 34 12 33 55 66 + * - +"
-3947
ghci> solveRPN "90 34 12 33 55 66 + * - + -"
4037
ghci> solveRPN "90 34 12 33 55 66 + * - + -"
4037
ghci> solveRPN "90 3 -"
87

¡Genial, funciona! Un detalle de esta función es que se puede modificar fácilmente para que soporte nuevos operadores. No tienen porque ser operadores binarios. Por ejemplo, podemos crear el operador "log" que solo retira un número de la pila y apila su logaritmo. También podemos crear operadores ternarios que retiren tres números de la pila y apilen un resultado, o operadores como sum que retiraría todos los números de la pila y devolvería su suma.

Vamos a modificar nuestra función para que acepte unos cuantos operadores más. Para simplificar, vamos a cambiar la declaración de tipo de forma que devuelva un número del tipo Float.

import Data.List

solveRPN :: String -> Float
solveRPN = head . foldl foldingFunction [] . words
    where   foldingFunction (x:y:ys) "*" = (x * y):ys
            foldingFunction (x:y:ys) "+" = (x + y):ys
            foldingFunction (x:y:ys) "-" = (y - x):ys
            foldingFunction (x:y:ys) "/" = (y / x):ys
            foldingFunction (x:y:ys) "^" = (y ** x):ys
            foldingFunction (x:xs) "ln" = log x:xs
            foldingFunction xs "sum" = [sum xs]
            foldingFunction xs numberString = read numberString:xs

¡Perfecto! ‘’/’’ es la división y ** la potencia de número en coma flotante. Con el operador logarítmico, usamos el ajuste de patrones para obtener un solo elemento y el resto de la lista, ya que solo necesitamos un elemento para obtener su logaritmo neperiano. Con el operador sum, devolvemos una pila con un solo elemento, el cual es la suma de toda la pila.

ghci> solveRPN "2.7 ln"
0.9932518
ghci> solveRPN "10 10 10 10 sum 4 /"
10.0
ghci> solveRPN "10 10 10 10 10 sum 4 /"
12.5
ghci> solveRPN "10 2 ^"
100.0

Fíjate que podemos incluir números en coma flotante en nuestra expresión porque read sabe como leerlos.

ghci> solveRPN "43.2425 0.5 ^"
6.575903

En mi opinión, crear una función que calcule expresiones arbitrarias RPN en coma flotante y tenga la opción de ser fácilmente extensible en solo 10 líneas es bastante impresionante.

Una cosa a tener en cuenta es que esta función no es tolerante a fallos. Cuando se da una entrada que no tiene sentido, simplemente bloqueará todo. Crearemos una versión tolerante a fallos de esta función con una declaración de tipo como solveRPN :: String -> Maybe Float una vez conozcamos las mónadas (no dan miedo, créeme). Podríamos crear una función como esta ahora mismo, pero sería un poco pesado ya que requeriría un montón de comprobaciones para Nothing en cada paso. Si crees que puede ser un reto, puedes continuar e intentarla crearla tu mismo. Un consejo: puedes utilizar reads para ver si una lectura a sido correcta o no.

De Heathrow a Londres¶

Nuestro siguiente problema es este: tu avión acaba de aterrizar en Inglaterra y alquilas un coche. Tienes una entrevista dentro de nada y tienes que llegar desde el aeropuerto de Heathrow a Londres tan pronto como puedas (¡Pero si arriesgar tu vida!).

Existen dos vías principales de Heathrow a Londres y hay cierto número de carreteras regionales que unen ambas vías. Debes encontrar la ruta óptima que te lleve a Londres tan rápido como puedas. Empiezas en el lado izquierdo y puedes o bien cruzar a la otra vía o continuar recto.

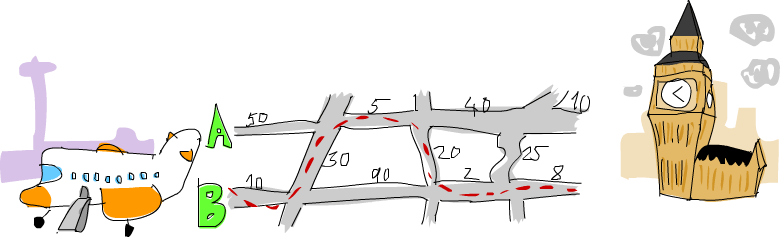
Como puedes ver en la imagen, la ruta más corta de Heathrow a Londres en este caso es empezando en la vía principal B, cruzamos y continuamos por A, cruzamos otra vez y continuamos dos veces más por B. Si tomamos esta ruta, tardaremos 75 minutos en llegar. Si tomamos cualquier otra ruta, tardaríamos más en llegar.

Nuestro trabajo es crear un programa que tome una entrada que represente un sistema de caminos y muestre cual es la ruta más corta. Así se vería la entrada para este caso.

Para analizar mentalmente el fichero de entrada, separa los números en grupos de tres. Cada grupo se compone de la vía A, la vía B y un camino que los une. Para que encajen perfectamente en grupos de tres, diremos que hay un último camino de cruce que recorrerlo toma cero minutos. Esto se debe a que no nos importa a que parte de Londres lleguemos, mientras lleguemos a Londres.

De la misma forma que solucionamos el problema de la calculadora RPN, este problema lo resolveremos en tres pasos:

Olvida Haskell por un instante y piensa como solucionarías el problema a mano.

Piensa como vamos a representar la información en Haskell.

Encuentra un modo de operar sobre esta información en Haskell que produzca una solución.

En el problema de la calculadora, primero nos dimos cuenta de que cuando calculábamos una expresión a mano, manteníamos una especie de pile en nuestra cabeza y recorríamos la expresión elemento a elemento. Decidimos utilizar una lista de cadenas para representar la expresión. Para terminar, utilizamos un pliegue por la izquierda para recorrer la lista de cadenas mientras manteníamos un pila que producía una solución.

Vale ¿Cómo encontraríamos la ruta más corta de Heathrow a Londres a mano? Bueno, podemos simplemente ver todas las rutas y suponer cual será la más corta y seguramente sea verdad. Esa solución funciona bien para problemas pequeños, pero ¿Qué pasaría si las vías tuvieran más de 10.000 secciones? Ni siquiera podríamos dar una solución optima.

Así que no es una buena solución. Aquí tienes una imagen simplificada del sistema de caminos:

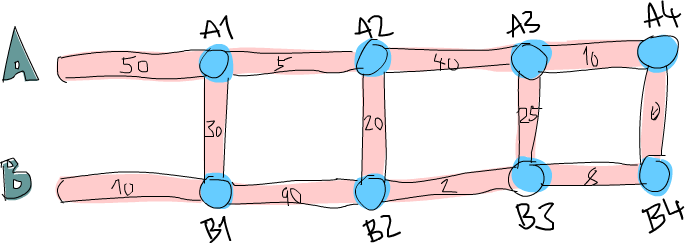
Esta bien ¿Puedes decir cual sería la ruta más corta hasta la primera intersección (El primer punto en A, marcado como A1) de la vía A? Es bastante trivial. Simplemente vemos si es mas corto ir recto desde A o si es más corto partir desde B y luego cruzar a la otra vía. Obviamente, es más corto ir por B y luego cruzar ya que toma 40 minutos, mientras que ir directamente desde A toma 50 minutos ¿Qué pasaría si quisiéramos ir a B1? Lo mismo. Vemos que es mucho más corto ir directamente desde B (10 minutos), ya que ir desde A y luego cruzan nos llevaría un total de 80 minutos.

Ahora sabemos la ruta más corta hasta A1 (ir desde la vía B y cruzar, diríamos algo como que es B, C con un coste de 40) y sabemos cual es la ruta más corta hasta B1 (ir directamente desde la vía B, simplemente B con coste 10) ¿Nos ayudaría en algo esta información si queremos saber la ruta más corta hasta la próxima intersección de ambas vías principales? ¡Por supuesto que sí!

Vamos a ver cual sería la ruta más corta hasta A2. Para llegar a A2, o bien iríamos directamente desde A1 o bien partiríamos desde B1, continuaríamos adelante y luego cruzaríamos (recuerda, solo podemos ir adelante o cruzar al otro lado). Y como sabemos el coste de A1 y B1, podemos encontrar fácilmente cual será la ruta más corta de A1 a A2. Costaría 40 minutos llegar a A1 y luego otros 5 minutos en llegar desde A1 a A2, así que el resultado sería B, C, A con un coste de 45 minutos. Solo cuesta 10 minutos llegar hasta B1, pero luego costaría otros 110 minutos más para llegar hasta A2. Así que, de forma bastante obvia, la forma más rápida de llegar a A2 es B, C, A. Del mismo modo, la forma más rápida de llegar hasta B2 es continuar por A1 y luego cruzar.

Nota

¿Qué pasaría si para llegar a A2 primero cruzamos desde B1 y luego continuamos adelante? Bien, ya hemos cubierto la posibilidad de cruzar de B1 a A1 cuando buscábamos la mejor forma de llegar hasta A1, así que no tenemos que tomar en cuenta esta posibilidad en el siguiente paso.

Ahora que tenemos la mejor ruta para llegar hasta A2 y B2, podemos repetir este proceso indefinidamente hasta que alcancemos el final. Una vez tengamos las mejores rutas para llegar a A4 y B4, la mejor será la ruta óptima.

En el segundo paso básicamente hemos repetido lo que hicimos en el primer paso, solo que tuvimos en cuenta cuales fueron las mejores rutas para llegar a A y B. También podríamos decir que tomamos en cuenta las mejores rutas para llegar hasta A y B en el primer paso, solo que ambas rutas tendrían coste 0.

Así que en resumen, para obtener las mejor ruta ruta de Heathrow a Londres, hacemos esto: primero vemos cual es la mejor ruta hasta el próximo cruce de la vía principal A. Las dos opciones que tenemos son o bien ir directamente o bien empezar en la vía opuesta, continuar adelante y luego cruzar. Memorizamos la mejor ruta y el coste. Usamos el mismo método para ver cual es la mejor ruta hasta el próximo cruce desde B y la memorizamos. Luego, vemos si la ruta del siguiente cruce en A es mejor si la tomamos desde el cruce anterior en A o desde el cruce anterior en B y luego cruzar. Memorizamos la mejor ruta y hacemos lo mismo para la vía opuesta. Repetimos estos pasos hasta que alcancemos el final. La mejor de las dos rutas resultantes será la ruta óptima.

Básicamente lo que hacemos es mantener la mejor ruta por A y la mejor ruta por B hasta que alcancemos el final, y la mejor de ambas es el resultado. Sabemos como calcular la ruta más corta a mano. Si tuviéramos suficiente tiempo, papel y lápiz, podríamos calcular la ruta más corta de un sistema de caminos con cualquier número de secciones.

¡Siguiente paso! ¿Cómo representamos este sistema de caminos con los tipos de datos de Haskell? Una forma es ver los puntos iniciales y las intersecciones como nodos de un grafo que se conectan con otras intersecciones. Si imaginamos que los nodos iniciales en realidad se conectan con cada otro nodo con un camino, veríamos que cada nodo se conecta con el nodo del otro lado y con el nodo siguiente del mismo lado. Exceptuando los nodos finales, que únicamente se conectan con el nodo del otro lado.

data Node = Node Road Road | EndNode Road
data Road = Road Int Node

Un nodo es o bien un nodo normal que contiene información acerca del camino que lleva al otro nodo de la otra vía principal o del camino que lleva al siguiente nodo, o bien un nodo final, que solo contiene información acerca del camino que lleva al otro nodo de la otra vía principal. Un camino contiene la información que indica lo que se tarda en recorrerlo y el nodo al que lleva. Por ejemplo, la primera parte del camino de la vía A sería Road 50 a1 donde a1 sería un nodo Node x y, donde x e y serían los caminos a B1 y a A2.

Otra forma de representar el sistema sería utilizando Maybe para los caminos que llevan al siguiente nodo. Cada nodo tendría un camino que llevara a otro punto de la vía opuesta, pero solo los nodos que no están al final tendrían un camino que les llevará adelante.

data Node = Node Road (Maybe Road)
data Road = Road Int Node

Ambas son buenas formas de representar el sistema de caminos en Haskell y en realidad podríamos resolver el problema usándolas, pero, quizá podemos encontrar algo más simple. Si pensamos de nuevo en la forma de resolverlo a mano, vemos que en realidad siempre comprobamos los tiempos de los tres caminos de una sección a la vez: la parte del camino en la vía A, la parte opuesta en B y la parte C, que conecta ambas entre sí. Cuando estábamos buscando la ruta más corta entre A1 y B1, solo tuvimos que tratar con los tiempos de las primeras tres partes, los cuales eran 50, 10 y 30 minutos. Nos referiremos a esto como una sección. Así que el sistema de caminos que utilizamos para este ejemplo puede representarse fácilmente como cuatro secciones: 50, 10, 30, 5, 90, 20, 40, 2, 25 y 10, 8, 0.

Siempre es bueno mantener nuestros tipos de datos tan simple como sea posible, pero ¡No más simple!

data Section = Section { getA :: Int, getB :: Int, getC :: Int } deriving (Show)
type RoadSystem = [Section]

¡Es casi perfecto! Es simple y tengo la sensación de que va a funcionar perfectamente para la implementación de nuestra solución. Section es un tipo de dato algebraico simple que contiene tres enteros para los tiempos de los tres caminos de una sección. También hemos utilizado un sinónimo de tipo que dice que RoadSystem es una lista de secciones.

Nota

También podríamos haber utilizado una tripla como (Int, Int, Int) para representar una sección. Está bien utilizar tuplas en lugar de tipos de datos algebraicos propios para cosas pequeñas y puntuales, pero normalmente es mejor crear nuevos tipos para cosas como esta. De esta forma el sistema de tipos tiene más infomación acerca de que es cada cosa. Podemos utilizar (Int, Int, Int) para representar una sección de un camino o para representar un vector en un espacio tridimensional y podemos trabajar con ambos a la vez, pero de este modo podríamos acabar mezclandolos entre sí. Si utilizamos los tipos Section y Vector, no podremos, ni si quiera accidentalmente, sumar un vector a una sección.

Ahora el sistema de caminos de Heathrow a Londres se puede representar así:

heathrowToLondon :: RoadSystem
heathrowToLondon = [Section 50 10 30, Section 5 90 20, Section 40 2 25, Section 10 8 0]

Todo lo que nos queda por hacer es implementar la solución a la que llegamos con Haskell ¿Cual sería la declaración de tipo de una función que calcule el camino más corto para cualquier sistema de caminos? Tendría que tomar un sistema de caminos y devolver una ruta. Vamos a representar una ruta con una lista también. Crearemos el tipo Label que será una simple enumeración cuyos valores serán A, B o C. También crearemos un sinónimo de tipo: Path.

data Label = A | B | C deriving (Show)
type Path = [(Label, Int)]

Llamaremos a nuestra función optimalPath y tendrá una declaración de tipo como optimalPath :: RoadSystem -> Path. Si es llamada con el sistema heathrowToLondon deberá devolver una ruta como:

[(B,10),(C,30),(A,5),(C,20),(B,2),(B,8)]

Vamos a tener que recorrer la lista de secciones de izquierda a derecha y mantener un camino óptimo hasta A y un camino óptimo hasta B conforme vayamos avanzando. Acumularemos la mejor ruta conforme vayamos avanzando, de izquierda a derecha ¿A qué te suena esto? ¡Ding, ding, ding! ¡Correcto, es un pliegue por la izquierda!

Cuando resolvimos el problema a mano, había un paso que repetíamos una y otra vez. Requería comprobar el camino óptimo de A y B hasta el momento, además de la sección actual para producir un nuevo par de rutas óptimas hasta A y B. Por ejemplo, al principio la rutas óptimas son [] y [] para A y B. Analizamos la sección Section 50 10 30 y concluimos que la nueva ruta óptima para A es [(B,10),(C,30)] y que la nueva ruta óptima para B es [(B,10)]. Si vemos este paso como una función, tomaría un par de rutas y una sección y produciría un nuevo par de rutas. El tipo sería (Path, Path) -> Section -> (Path, Path). Vamos a seguir adelante e implementar esta función que parece que será útil.

Nota

Será util porque (Path, Path) -> Section -> (Path, Path) puede ser utilizado como una función binaría para un pliegue por la derecha, el cual tiene un tipo a -> b -> a.

roadStep :: (Path, Path) -> Section -> (Path, Path)
roadStep (pathA, pathB) (Section a b c) =
    let priceA = sum $ map snd pathA
        priceB = sum $ map snd pathB
        forwardPriceToA = priceA + a
        crossPriceToA = priceB + b + c
        forwardPriceToB = priceB + b
        crossPriceToB = priceA + a + c
        newPathToA = if forwardPriceToA <= crossPriceToA
                        then (A,a):pathA
                        else (C,c):(B,b):pathB
        newPathToB = if forwardPriceToB <= crossPriceToB
                        then (B,b):pathB
                        else (C,c):(A,a):pathA
    in  (newPathToA, newPathToB)

¿Qué hace esto? Primero, calculamos el coste óptimo en la vía A basandonos en el camino óptimo hasta el momento en A, y luego hacemos lo mismo para B. Hacemos sum $ map snd pathA, así que si pathA es algo como [(A,100),(C,20)], priceA será 120. forwardPriceToA es el coste de que tendría continuar hasta el siguiente cruce si fuéramos directamente desde el cruce anterior en A. Es igual al coste anterior de A, más el coste de la parte A de la sección actual. crossPriceToA es el coste que tendría si fuéramos hasta el siguiente cruce de A partiendo de B y luego cruzáramos. Este coste sería el coste óptimo de llegar al anterior cruce de B más el coste de continuar por B más el coste de cruzar por C. Calculamos forwardPriceToB y crossPriceToB de la misma forma.

Ahora que sabemos el mejor camino hasta A y B, solo tenemos que crear nuevas rutas para llegar hasta la siguiente intersección de A y B basándonos en estos. Si tardamos menos en llegar partiendo de A y continuando adelante, establecemos newPathToA a (A,a):pathA. Básicamente añadimos Label A y el coste de la sección a al camino óptimo de A hasta el momento. Dicho de otro modo, decimos que la mejor forma de llegar al siguiente cruce de A es la ruta de llegar al cruce de A anterior y luego continuando adelante por la vía A. Recuerda que es A es una simple etiqueta, mientras que a tiene el tipo Int ¿Por qué añadimos el nuevo elemento al inicio en lugar de hacer algo como pathA ++ [(A,a)]? Bueno, añadir un elemento al principio de una lista es mucho más rápido que añadirlo al final. De este modo la ruta estará invertida cuando terminemos el pliegue con esta función, pero podemos invertirla de nuevo luego. Si tardamos menos en llegar al siguiente cruce de A partiendo del cruce anterior en B y luego cruzando, entonces newPathToB será la ruta anterior por B, continuar adelante y cruzar a A. Hacemos lo mismo para newPathToB, solo que al revés.

Terminamos devolviendo newPathToA y newPathToB en una tupla.

Vamos a ejecutar esta función con la primera sección de heathrowToLondon. Como es la primera sección, las mejores rutas hasta A y B serán un par de listas vacías.

ghci> roadStep ([], []) (head heathrowToLondon)
([(C,30),(B,10)],[(B,10)])

Recuerda que las rutas están invertidas, así que léelas de derecha a izquierda. Podemos ver que la mejor ruta hasta el siguiente cruce en A es empezando por B y luego cruzar hasta A y que la mejor ruta hasta B es simplemente continuando adelante a partir de B.

Nota

Cuando hacemos priceA = sum $ map snd pathA, estamos calculando el coste de la ruta en cada paso. No tendríamos que hacerlo si implementamos roadStep como una función (Path, Path, Int, Int) -> Section -> (Path, Path, Int, Int) donde los enteros representan el coste de A y B.

Ahora que tenemos una función que toma un par de rutas y una sección y produce una nueva ruta óptima, podemos hacer fácilmente un pliegue por la izquierda de la lista de secciones. roadStep se llamará con ([],[]) y la primera sección y devolverá una dupla con las rutas óptimas para esa sección. Luego será llamada con esa dupla de rutas y la sección siguiente y así sucesivamente. Cuando hayamos recorrido todas las secciones, tendremos una dupla con las rutas óptimas, y la mas corta será nuestra respuesta. Tendiendo esto en cuenta, podemos implementar optimalPath.

optimalPath :: RoadSystem -> Path
optimalPath roadSystem =
    let (bestAPath, bestBPath) = foldl roadStep ([],[]) roadSystem
    in  if sum (map snd bestAPath) <= sum (map snd bestBPath)
            then reverse bestAPath
            else reverse bestBPath

Plegamos roadSystem por la izquierda (recuerda, es una lista de secciones) con un acumulador inicial que es una dupla de listas vacías. El resultado de ese pliegue es una dupla de rutas, así que usamos un ajuste de patrones sobre ella y obtenemos las rutas. Luego, comprobamos cual de esas dos es mejor y la devolvemos. Antes de devolverla, la invertimos, ya que las rutas óptimas están al revés debido a que decidimos añadir las secciones al principio de las listas.

¡Vamos a probarla!

ghci> optimalPath heathrowToLondon
[(B,10),(C,30),(A,5),(C,20),(B,2),(B,8),(C,0)]

¡Este es el resultado que se supone que debíamos obtener! ¡Genial! Se diferencia un poco del resultado que esperábamos ya que hay un paso (C,0) al final, lo que significa que tomamos un cruce cuando ya estamos en Londres, pero como tomar dicho camino no cuesta nada, sigue siendo la solución correcta.

Ahora que ya tenemos la función que encuentra la ruta óptima, solo tenemos que leer la representación textual del sistema de caminos por la entrada estándar, convertirlo en el tipo RoadSystem, ejecutar optimalPath sobre él y mostrar el resultado.

Antes de nada, vamos a crear una función que tome una lista y la divida en grupos del mismo tamaño. La llamaremos groupsOf. Con un parámetro como [1..10], groupsOf 3 deberá devolver [[1,2,3],[4,5,6],[7,8,9],[10]].

groupsOf :: Int -> [a] -> [[a]]
groupsOf 0 _ = undefined
groupsOf _ [] = []
groupsOf n xs = take n xs : groupsOf n (drop n xs)

Una función recursiva estándar. Para un xs de [1..10] y un n de 3, equivale a [1,2,3] : groupsOf 3 [4,5,6,7,8,9,10]. Cuando la recursión termina, obtenemos una lista de grupos de tres elementos. Y aquí esta la función main, la cual leer desde la entrada estándar, crea un RoadSystem y muestra la ruta más corta:

import Data.List

main = do
    contents <- getContents
    let threes = groupsOf 3 (map read $ lines contents)
        roadSystem = map (\[a,b,c] -> Section a b c) threes
        path = optimalPath roadSystem
        pathString = concat $ map (show . fst) path
        pathPrice = sum $ map snd path
    putStrLn $ "The best path to take is: " ++ pathString
    putStrLn $ "The price is: " ++ show pathPrice

Primero, obtenemos todos los contenidos de la entrada estándar. Luego llamamos a lines con los contenidos para convertir algo como "50\n10\n30\n... en ["50","10","30"... y luego mapeamos read sobre ella para obtener una lista de números. También llamamos a groupsOf 3 sobre ella de forma que obtengamos una lista de listas de longitud tres. Mapeamos la función lambda (\[a,b,c] -> Section a b c) sobre esta lista de listas. Como puedes ver, esta función lambda toma una lista de tamaño tres y devuelve una sección. Así que roadSystem es nuestro sistema de caminos e incluso tiene el tipo correcto, RoadSystem (o [Section]). Llamamos optimalPath sobre éste y mostramos la ruta y el coste de la ruta óptima que obtenemos.

Guardamos el siguiente texto:

En un fichero llamado paths.txt y luego se lo pasamos a nuestro programa.

$ cat paths.txt | runhaskell heathrow.hs
The best path to take is: BCACBBC
The price is: 75

¡Funciona perfecto! Puedes usar tu conocimiento del módulo Data.Random para generar un sistema de caminos mucho más grande, que luego podrás pasar a nuestro programa de la misma forma que hemos hecho. Si obtienes errores de desbordamiento de pila, intenta usar foldl' en lugar foldl, ya que foldl' es estricto.

Navegación

Resolviendo problemas de forma funcional¶

Notación polaca inversa¶

De Heathrow a Londres¶

Navegación