Recursión

¡Hola recursión!

En el capítulo anterior ya mencionamos la recursión. En este capítulo veremos más detenidamente este tema, el porqué es importante en Haskell y como podemos crear soluciones a problemas de forma elegante y concisa.

Si aún no sabes que es la recursión, lee esta frase: La recursión es en realidad una forma de definir funciones en la que dicha función es utiliza en la propia definición de la función. Las definiciones matemáticas normalmente están definidas de forma recursiva. Por ejemplo, la serie de Fibonacci se define recursivamente. Primero, definimos los dos primeros números de Fibonacci de forma no recursiva. Decimos que F(0) = 0 y F(1) = 1, que significa que el 1º y el 2º número de Fibonacci es 0 y 1, respectivamente. Luego, para cualquier otro índice, el número de Fibonacci es la suma de los dos números de Fibonacci anteriores. Así que F(n) = F(n-1) + F(n-2). De esta forma, F(3) = F(2) + F(1) que es F(3) = (F(1) + F(0)) + F(1). Como hemos bajado hasta los únicos números definidos no recursivamente de la serie de Fibonacci, podemos asegurar que F(3) = 2. Los elementos definidos no recursivamente, como F(0) o F(1), se llaman casos base, y si tenemos solo casos base en una definición como en F(3) = (F(1) + F(0)) + F(1) se denomina condición límite, la cual es muy importante si quieres que tu función termine. Si no hubiéramos definido F(0) y F(1) no recursivamente, nunca obtendríamos un resultado para un número cualquiera, ya que alcanzaríamos 0 y continuaríamos con los número negativos. De repente, encontraríamos un F(-2000) = F(-2001) + F(-2002) y seguiríamos sin ver el final.

La recursión es muy importante en Haskell ya que, al contrario que en los lenguajes imperativos, realizamos cálculos declarando como es algo, en lugar de declarar como obtener algo. Por este motivo no hay bucles while o bucles for en Haskell y en su lugar tenemos que usar la recursión para declarar como es algo.

El impresionante maximum

La función maximum toma una lista de cosas que pueden ser ordenadas (es decir instancias de la clase de tipos Ord) y devuelve la más grande. Piensa en como implementaríamos esto de forma imperativa. Probablemente crearíamos una variable para mantener el valor máximo hasta el momento y luego recorreríamos los elementos de la lista de forma que si un elemento es mayor que el valor máximo actual, lo remplazaríamos. El máximo valor que se mantenga al final es el resultado. ¡Wau! son muchas palabras para definir un algoritmo tan simple.

Ahora vamos a ver como definiríamos esto de forma recursiva. Primero podríamos establecer un caso base diciendo que el máximo de una lista unitaria es el único elemento que contiene la lista. Luego podríamos decir que el máximo de una lista más larga es la cabeza de esa lista si es mayor que el máximo de la cola, o el máximo de la cola en caso de que no lo sea. ¡Eso es! Vamos a implementarlo en Haskell.

maximum' :: (Ord a) => [a] -> a
maximum' [] = error "Máximo de una lista vacía"
maximum' [x] = x
maximum' (x:xs)
    | x > maxTail = x
    | otherwise   = maxTail
    where maxTail = maximum' xs

Como puedes ver el ajuste de patrones funcionan genial junto con la recursión. Muchos lenguajes imperativos no tienen patrones así que hay que utilizar muchos if/else para implementar los casos base. El primer caso base dice que si una lista está vacía, ¡Error! Tiene sentido porque, ¿cuál es el máximo de una lista vacía? Ni idea. El segundo patrón también representa un caso base. Dice que si nos dan una lista unitaria simplemente devolvemos el único elemento.

En el tercer patrón es donde está la acción. Usamos un patrón para dividir la lista en cabeza y cola. Esto es algo muy común cuando usamos una recursión con listas, así que ve acostumbrándote. Usamos una sección where para definir maxTail como el máximo del resto de la lista. Luego comprobamos si la cabeza es mayor que el resto de la cola. Si lo es, devolvemos la cabeza, si no, el máximo del resto de la lista.

Vamos a tomar una lista de números de ejemplo y comprobar como funcionaria: [2,5,1]. Si llamamos maximum' con esta lista, los primeros dos patrones no ajustarían. El tercero si lo haría y la lista se dividiría en 2 y [5,1]. La sección where requiere saber el máximo de [5,1] así que nos vamos por ahí. Se ajustaría con el tercer patrón otra vez y [5,1] sería dividido en 5 y [1]. Otra vez, la sección where requiere saber el máximo de [1]. Como esto es un caso base, devuelve 1 ¡Por fin! Así que subimos un paso, comparamos 5 con el máximo de [1] (que es 1) y sorprendentemente obtenemos 5. Así que ahora sabemos que el máximo de [5,1] es 5. Subimos otro paso y tenemos 2 y [5,1]. Comparamos 2 con el máximo de [5,1], que es 5 y elegimos 5.

Una forma más clara de escribir la función maximum' es usando la función max. Si recuerdas, la función max toma dos cosas que puedan ser ordenadas y devuelve la mayor de ellas. Así es como podríamos reescribir la función utilizando max:

maximum' :: (Ord a) => [a] -> a
maximum' []     = error "maximum of empty list"
maximum' [x]    = x
maximum' (x:xs) = x `max` (maximum' xs)

¿A que es elegante? Resumiendo, el máximo de una lista es el máximo entre su primer elemento y el máximo del resto de sus elementos.

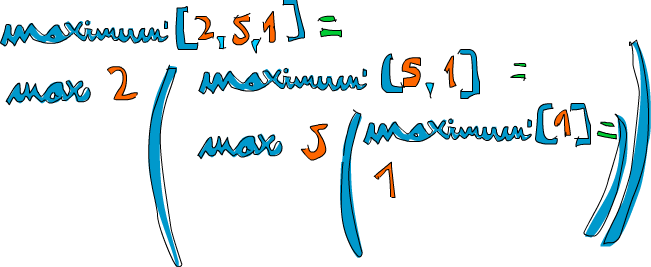
Unas cuantas funciones recursivas más

Ahora que sabemos cómo pensar de forma recursiva en general, vamos a implementar unas cuantas funciones de forma recursiva. En primer lugar, vamos a implementar replicate. replicate toma un Int y algún elemento y devuelve una lista que contiene varias repeticiones de ese mismo elemento. Por ejemplo, replicate 3 5 devuelve [5,5,5]. Vamos a pensar en el caso base. Mi intuición me dice que el caso base es 0 o menos. Si intentamos replicar algo 0 o menos veces, debemos devolver una lista vacía. También para números negativos ya que no tiene sentido.

replicate' :: (Num i, Ord i) => i -> a -> [a]
replicate' n x
    | n <= 0    = []
    | otherwise = x:replicate' (n-1) x

Aquí usamos guardas en lugar de patrones porque estamos comprobando una condición booleana. Si n es menor o igual que 0 devolvemos una lista vacía. En otro caso devolvemos una lista que tiene x como primer elemento y x replicado n-1 veces como su cola. Finalmente, la parte n-1 hará que nuestra función alcance el caso base.

Ahora vamos a implementar take. Esta función toma un cierto número de elementos de una lista. Por ejemplo, take 3 [5,4,3,2,1] devolverá [5,4,3]. Si intentamos obtener 0 o menos elementos de una lista, obtendremos una lista vacía. También si intentamos tomar algo de una lista vacía, obtendremos una lista vacía. Fíjate que ambos son casos base. Vamos a escribirlo.

take' :: (Num i, Ord i) => i -> [a] -> [a]
take' n _
    | n <= 0   = []
take' _ []     = []
take' n (x:xs) = x : take' (n-1) xs

El primer patrón indica que si queremos obtener 0 o un número negativo de elementos, obtenemos una lista vacía. Fíjate que estamos usando _ para enlazar la lista ya que realmente no nos importa en este patrón. Además también estamos usando una guarda, pero sin la parte otherwise. Esto significa que si n acaba siendo algo más que 0, el patrón fallará y continuará hacia el siguiente. El segundo patrón indica que si intentamos tomar algo de una lista vacía, obtenemos una lista vacía. El tercer patrón rompe la lista en cabeza y cola. Luego decimos que si tomamos n elementos de una lista es igual a una lista que tiene x como cabeza y como cola una lista que tome n-1 elementos de la cola. Intenta usar papel y lápiz para seguir el desarrollo de como sería la evaluación de take 3 [4,3,2,1], por ejemplo.

reverse simplemente pone al revés una lista. Piensa en el caso base, ¿cuál es? Veamos... ¡Es una lista vacía! Una lista vacía inversa es igual a esa misma lista vacía. Vale, ¿qué hay del resto de la lista? Podríamos decir que si dividimos una lista en su cabeza y cola, la lista inversa es igual a la cola invertida más luego la cabeza al final.

reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x:xs) = reverse' xs ++ [x]

¡Ahí lo tienes!

Como Haskell soporta listas infinitas, en realidad nuestra recursión no tiene porque tener casos base. Pero si no los tiene, seguiremos calculando algo infinitamente o bien produciendo una estructura infinita. Sin embargo, lo bueno de estas listas infinitas es que podemos cortarlas por donde queramos. repeat toma un elemento y devuelve una lista infinita que simplemente tiene ese elemento. Una implementación recursiva extremadamente simple es:

repeat' :: a -> [a]
repeat' x = x : repeat' x

Llamando a repeat 3 nos daría una lista que tiene un 3 en su cabeza y luego tendría una lista infinita de treses en su cola. Así que repeat 3 se evaluaría a algo como 3:(repeat 3), que es 3:(3:(repeat 3)), que es 3:(3:(3:(repeat 3))), etc. repeat 3 nunca terminará su evaluación, mientras que take 5 (repeat 3) nos devolverá un lista con cinco treses. Es igual que hacer replicate 5 3.

zip toma dos listas y las combina en una. zip [1,2,3] [2,3] devuelve [(1,2),(2,3)] ya que trunca la lista más larga para que coincida con la más corta. ¿Qué pasa si combinamos algo con la lista vacía? Bueno, obtendríamos un una lista vacía. Así que es este es nuestro caso base. Sin embargo, zip toma dos listas como parámetros, así que en realidad tenemos dos casos base.

zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys

Los dos primeros patrones dicen que si la primera o la segunda lista están vacías entonces obtenemos una lista vacía. Combinar [1,2,3] y ['a','b'] finalizará intentando combinar [3] y []. El caso base aparecerá en escena y el resultado será (1,'a'):(2,'b'):[] que exactamente lo mismo que [(1,'a'),(2,'b')].

Vamos a implementar una función más de la biblioteca estándar, elem, que toma un elemento y una lista y busca si dicho elemento está en esa lista. El caso base, como la mayoría de las veces con las listas, es la lista vacía. Sabemos que una lista vacía no contiene elementos, así que lo más seguro es que no contenga el elemento que estamos buscando...

elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
    | a == x    = True
    | otherwise = a `elem'` xs

Bastante simple y previsible. Si la cabeza no es elemento que estamos buscando entonces buscamos en la cola. Si llegamos a una lista vacía, el resultado es falso.

¡Quicksort!

Tenemos una lista de elementos que pueden ser ordenados. Su tipo es miembro de la clase de tipos Ord. Y ahora, queremos ordenarlos. Existe un algoritmo muy interesante para ordenarlos llamado Quicksort. Es una forma muy inteligente de ordenar elementos. Mientras en algunos lenguajes imperativos puede tomar hasta 10 líneas de código para implementar Quicksort, en Haskell la implementación es mucho más corta y elegante. Quicksort se ha convertido en usa especie de pieza de muestra de Haskell. Por lo tanto, vamos a implementarlo, a pesar de que la implementación de Quicksort en Haskell se considera muy cursi ya que todo el mundo lo hace en las presentaciones para que veamos los bonito que es.

Bueno, la declaración de tipo será quicksort :: (Ord a) => [a] -> [a]. Ninguna sorpresa. ¿Caso base? La lista vacía, como era de esperar. Ahora viene el algoritmo principal: una lista ordenada es una lista que tiene todos los elementos menores (o iguales) que la cabeza al principio (y esos valores están ordenados), luego viene la cabeza de la lista que estará en el medio y luego vienen los elementos que son mayores que la cabeza (que también estarán ordenados). Hemos dicho dos veces “ordenados”, así que probablemente tendremos que hacer dos llamadas recursivas. También hemos usado dos veces el verbo “es” para definir el algoritmo en lugar de “hace esto”, “hace aquello”, “entonces hace”... ¡Esa es la belleza de la programación funcional! ¿Cómo vamos a conseguir filtrar los elementos que son mayores y menores que la cabeza de la lista? Con listas intensionales. Así que empecemos y definamos esta función:

quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) =
    let smallerSorted = quicksort [a | a <- xs, a <= x]
        biggerSorted  = quicksort [a | a <- xs, a > x]
    in  smallerSorted ++ [x] ++ biggerSorted

Vamos a ejecutar una pequeña prueba para ver si se comporta correctamente.

ghci> quicksort [10,2,5,3,1,6,7,4,2,3,4,8,9]
[1,2,2,3,3,4,4,5,6,7,8,9,10]
ghci> quicksort "el veloz murcielago hindu comia feliz cardillo y kiwi"
"        aaacccddeeeefghiiiiiiikllllllmmnoooorruuvwyzz"

Bien ¡De esto estábamos hablando! Así que si tenemos, digamos [5,1,9,4,6,7,3] y queremos ordenarlos, el algoritmo primero tomará la cabeza de la lista, que es 5 y lo pondrá en medio de dos listas que son los menores y los mayores de este. De esta forma tendremos (quicksort [1,4,3]) ++ [5] ++ (quicksort [9,6,7]). Sabemos que cuando la lista este completamente ordenada, el número 5 permanecerá en la cuarta posición ya que hay tres números menores y tres números mayores que él. Ahora si ordenamos [1,4,3] y [9,6,7], ¡tendremos una lista ordenada! Ordenamos estas dos listas utilizando la misma función. Al final llegaremos a un punto en el que alcanzaremos listas vacías y las listas vacías ya están ordenadas de alguna forma. Aquí tienes una ilustración:

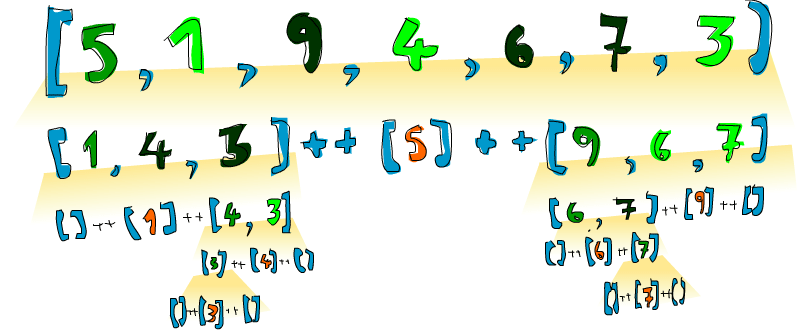
Un elemento que está en su posición correcta y no se moverá más está en naranja. Leyendo de izquierda a derecha estos elemento la lista aparece ordenada. Aunque elegimos comparar todos los elementos con la cabeza, podríamos haber elegido cualquier otro elemento. En Quicksort, se llama pivote al elemento con el que comparamos. Estos son los de color verde. Elegimos la cabeza porque es muy fácil aplicarle un patrón. Los elementos que son más pequeños que el pivote son de color verde claro y los elementos que son mayores en negro. El gradiente amarillo representa la aplicación de Quicksort.

Pensando de forma recursiva

Hemos usado un poco la recursión y como te habrás dado cuenta existen unos pasos comunes. Normalmente primero definimos los casos base y luego definimos una función que hace algo entre un elemento y la función aplicada al resto de elementos. No importa si este elemento es una lista, un árbol o cualquier otra estructura de datos. Un sumatorio es la suma del primer elemento más la suma del resto de elementos. Un productorio es el producto del primer elemento entre el producto del resto de elementos. El tamaño de una lista es 1 más el tamaño del resto de la lista, etc.

Por supuesto también existen los casos base. Por lo general un caso base es un escenario en el que la aplicación de una recursión no tiene sentido. Cuando trabajamos con listas, los casos base suelen tratar con listas vacías. Cuando utilizamos árboles los casos base son normalmente los nodos que no tienen hijos.

Es similar cuando tratamos con números. Normalmente hacemos algo con un número y luego aplicamos la función a ese número modificado. Ya hicimos funciones recursivas de este tipo como el del factorial de un número, el cual no tiene sentido con cero, ya que el factorial solo está definido para enteros positivos. A menudo el caso base resulta ser la identidad. La identidad de la multiplicación es 1 ya que si multiplicas algo por 1 obtienes el mismo resultado. También cuando realizamos sumatorios de listas, definimos como 0 al sumatorio de una lista vacía, ya que 0 es la identidad de la suma. En Quicksort, el caso base es la lista vacía y la identidad es también la lista vacía, ya que si añades a una lista la lista vacía obtienes la misma lista ordenada.

Cuando queremos resolver un problema de forma recursiva, primero pensamos donde no se aplica una solución recursiva y si podemos utilizar esto como un caso base. Luego pensamos en las identidades, por donde deberíamos romper los parámetros (por ejemplo, las lista se rompen en cabeza y cola) y en que parte deberíamos aplicar la función recursiva.