Zippers

Mientras que la pureza de Haskell nos da un montón de beneficios, nos hace abordar algunos problemas de forma muy diferente a como lo haríamos en otros lenguajes impuros. Debido a la transparencia referencial de Haskell, un valor es exactamente igual a otro si ambos representan lo mismo.

Si tenemos tres árboles llenos de cincos y queremos cambiar uno de ellos a seis, tenemos que tener algún modo de decir qué cinco en concreto del árbol queremos modificar. Tenemos que conocer la posición que ocupa en el árbol. En los lenguajes imperativos podemos ver en que parte de la memoria se encuentra el cinco que queremos modificar y ya esta. Pero en Haskell, un cinco es exactamente igual a cualquier otro cinco, así que no podemos elegir uno basándonos en que posición ocupa en la memoria. Tampoco podemos cambiar nada. Cuando decimos que vamos a modificar un árbol, en realidad significa que vamos a tomar un árbol y devolver uno nuevo que será similar al original, pero algo diferente.

Una cosa que podemos hacer es recordar el camino que seguimos para llegar al elemento que queremos modificar desde la raíz del árbol. Podríamos decir, toma este árbol, vez a la izquierda, ves a la derecha, vuelve a ir a la izquierda y modifica el elemento que se encuentre allí. Aunque esto funcionaría, puede ser ineficiente. Si luego queremos modificar un elemento que se encuentra al lado del elemento que acabamos de modificar, tenemos que recorrer de nuevo todo el camino empezando por la raíz.

En este capítulo veremos como podemos tomar una estructura de datos cualquiera y centrarnos en la forma en la que modificamos y nos desplazamos por sus elementos de forma eficiente.

Dando un paseo

Como aprendimos en clase de ciencias naturales, existen mucho tipos de árboles diferentes, así que vamos a elegir una semilla y plantar el nuestro. Aquí la tienes:

data Tree a = Empty | Node a (Tree a) (Tree a) deriving (Show)

Así que este árbol es o bien Empty o bien es un nodo que contiene dos sub-árboles. Aquí tienes un ejemplo de árbol de este tipo, ¡gratis!

freeTree :: Tree Char
freeTree =
    Node 'P'
        (Node 'O'
            (Node 'L'
                (Node 'N' Empty Empty)
                (Node 'T' Empty Empty)
            )
            (Node 'Y'
                (Node 'S' Empty Empty)
                (Node 'A' Empty Empty)
            )
        )
        (Node 'L'
            (Node 'W'
                (Node 'C' Empty Empty)
                (Node 'R' Empty Empty)
            )
            (Node 'A'
                (Node 'A' Empty Empty)
                (Node 'C' Empty Empty)
            )
        )

Y así es su representación gráfica/artística:

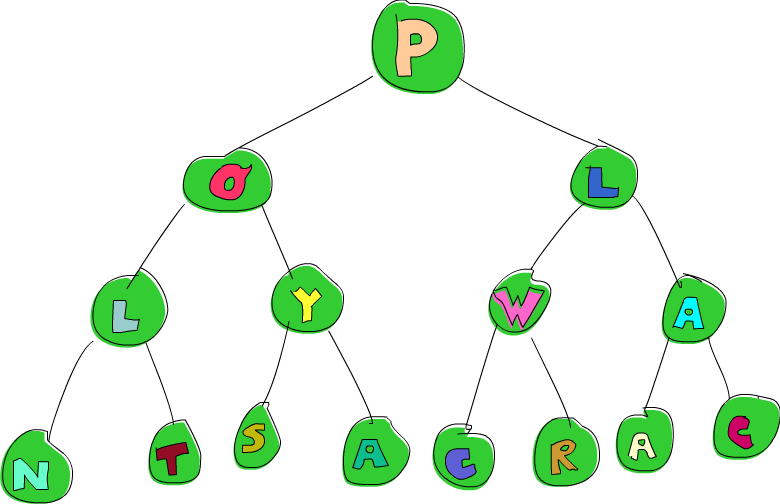
¿Ves esa W? Digamos que queremos cambiarla por una P ¿Cómo lo hacemos? Bueno, una forma sería utilizando un ajuste de patrones sobre el árbol hasta que encontremos el elemento que buscamos, es decir, vamos por la derecha, luego por la izquierda y modificamos el elemento. Así sería:

changeToP :: Tree Char -> Tree Char
changeToP (Node x l (Node y (Node _ m n) r)) = Node x l (Node y (Node 'P' m n) r)

¡Aarg! No solo es feo si no también algo confuso ¿Qué hace esto? Bueno, utilizamos un ajuste de patrones sobre el árbol y llamamos a su elemento raíz x (que en este caso será 'P') y su sub-árbol izquierdo l. En lugar de dar un nombre a su sub-árbol derecho, utilizamos otro patrón sobre él. Continuamos ese ajuste de patrones hasta que alcanzamos el sub-árbol cuya raíz es 'W'. Una vez hemos llegado, reconstruimos el árbol, solo que en lugar de que ese sub-árbol contenga una 'W' contendrá una 'P'.

¿Existe alguna forma de hacer esto mejor? Podríamos crear una función que tome un árbol junto a una lista de direcciones. Las direcciones será o bien L (izquierda) o bien R (derecha), de forma que cambiamos el elemento una vez hemos seguido todas las direcciones.

data Direction = L | R deriving (Show)
type Directions = [Direction]

changeToP :: Directions-> Tree Char -> Tree Char
changeToP (L:ds) (Node x l r) = Node x (changeToP ds l) r
changeToP (R:ds) (Node x l r) = Node x l (changeToP ds r)
changeToP [] (Node _ l r) = Node 'P' l r

Si el primer elemento de la lista de direcciones es L, creamos un árbol que igual al anterior solo que su sub-árbol izquierdo ahora contendrá el elemento modificado a P. Cuando llamamos recursivamente a changeToP, le pasamos únicamente la cola de la listas de direcciones, porque sino volvería a tomar la misma dirección. Hacemos lo mismo en caso de R. Si la lista de direcciones está vacía, significa que hemos alcanzado nuestro destino, así que devolvemos un árbol idéntico al que hemos recibido, solo que este nuevo árbol tendrá 'P' como elemento raíz.

Para evitar tener que mostrar el árbol entero, vamos a crear una función que tome una lista de direcciones y nos devuelva el elemento que se encuentra en esa posición.

elemAt :: Directions -> Tree a -> a
elemAt (L:ds) (Node _ l _) = elemAt ds l
elemAt (R:ds) (Node _ _ r) = elemAt ds r
elemAt [] (Node x _ _) = x

Esta función es muy parecida a changeToP, solo que en lugar de reconstruir el árbol paso a paso, ignora cualquier cosa excepto su destino. Vamos a cambiar 'W' por 'P' y luego comprobaremos si el árbol se ha modificado correctamente:

ghci> let newTree = changeToP [R,L] freeTree
ghci> elemAt [R,L] newTree
'P'

Genial, parece que funciona. En estas funciones, la lista de direcciones actúa como especie de objetivo, ya que señala un sub-árbol concreto del árbol principal. Por ejemplo, una lista de direcciones como [R] señala el sub-árbol izquierdo que cuelga de la raíz. Una lista de direcciones vacía señala el mismo árbol principal.

Aunque estas técnicas parecen correctas, pueden ser más bien ineficientes, especialmente si queremos modificar elementos de forma repetida. Digamos que tenemos un árbol inmenso y una larga lista de direcciones que señala un elemento que se encuentra al final del árbol. Utilizamos esta lista de direcciones para recorrer el árbol y modificar dicho elemento. Si queremos modificar un elemento que se encuentra cerca del elemento que acabamos de modificar, tenemos que empezar otra ves desde la raíz del árbol y volver a recorrer de nuevo todo el camino.

En la siguiente sección veremos un forma mejor de señalar un sub-árbol, una que nos permita señalar de forma eficiente a los sub-árbol vecinos.

Un rastro de migas

Vale, así que para centrarnos o señalar un solo sub-árbol, buscamos algo mejor que una simple lista de direcciones que parta siempre desde la raíz ¿Ayudaría si comenzamos desde la raíz y nos movemos a la izquierda o la derecha y al mismo tiempo dejáramos una especie de rastro? Es decir, si vamos a la izquierda, recordamos que hemos ido por la izquierda, y si vamos por la derecha, recordamos que hemos ido por la derecha. Podemos intentarlo.

Para representar este rastro, usaremos también una lista de direcciones (es decir, o bien L o bien R), solo que en lugar de llamarlo Directions (direcciones) lo llamaremos Breadcrumbs (rastro), ya que iremos dejando las direcciones que hemos tomado a lo largo del camino.

type Breadcrumbs = [Direction]

Aquí tienes una función que toma un árbol y un rastro y se desplaza al sub-árbol izquierdo añadiendo L a la cabeza de la lista que representa el rastro:

goLeft :: (Tree a, Breadcrumbs) -> (Tree a, Breadcrumbs)
goLeft (Node _ l _, bs) = (l, L:bs)

Ignoramos el elemento raíz y el sub-árbol derecho y simplemente devolvemos el sub-árbol izquierdo junto al rastro anterior añadiéndole L. Aquí tienes la función que se desplaza a la derecha:

goRight :: (Tree a, Breadcrumbs) -> (Tree a, Breadcrumbs)
goRight (Node _ _ r, bs) = (r, R:bs)

Funciona del mismo modo. Vamos a utilizar estas funciones para tomen el árbol freeTree y se desplacen primero a la derecha y luego a la izquierda.

ghci> goLeft (goRight (freeTree, []))
(Node 'W' (Node 'C' Empty Empty) (Node 'R' Empty Empty),[L,R])

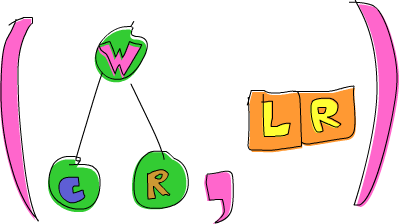
Vale, ahora tenemos un árbol que tiene 'W' como elemento raíz, 'C' como sub-árbol izquierdo y 'R' como sub-árbol derecho. El rastro es [L,R] porque primero fuimos a la derecha y luego a la izquierda.

Para que recorrer el árbol sea más cómodo vamos crear la función -: que definiremos así:

x -: f = f x

La cual nos permite aplicar funciones a valores escribiendo primero el valor, luego -: y al final la función. Así que en lugar de hacer goRight (freeTree, []), podemos escribir (freeTree, []) -: goRight. Usando esta función podemos reescribir el código anterior para parezca más que primero vamos a la derecha y luego a la izquierda:

ghci> (freeTree, []) -: goRight -: goLeft
(Node 'W' (Node 'C' Empty Empty) (Node 'R' Empty Empty),[L,R])

Volviendo atrás

¿Qué pasa si queremos volver por el camino que hemos tomado? Gracias al rastro sabemos que el árbol actual es el sub-árbol izquierdo del sub-árbol derecho que colgaba del árbol principal, pero nada más. No nos dice nada acerca del padre del sub-árbol actual para que podamos volver hacia arriba. Parece que aparte del las direcciones que hemos tomado, el rastro también debe contener toda la información que desechamos por el camino. En este caso, el sub-árbol padre que contiene también el sub-árbol izquierdo que no tomamos.

En general, un solo rastro debe contener toda la información suficiente para poder reconstruir el nodo padre. De esta forma, tenemos información sobre todas las posibles rutas que no hemos tomado y también conocemos el camino que hemos tomado, pero debe contener información acerca del sub-árbol en el que nos encontramos actualmente, si no, estaríamos duplicando información.

Vamos a modificar el tipo rastro para que también contenga la información necesaria para almacenar todos los posibles caminos que vamos ignorando mientras recorremos el árbol. En lugar de utilizar Direction, creamos un nuevo tipo de datos:

data Crumb a = LeftCrumb a (Tree a) | RightCrumb a (Tree a) deriving (Show)

Ahora, en lugar de tener únicamente L, tenemos LeftCrumb que contiene también el nodo desde el cual nos hemos desplazado y el sub-árbol derecho que no hemos visitado. En lugar de R, ahora tenemos RightCrumb que contiene el nodo desde el cual nos hemos desplazado y el sub-árbol izquierdo que hemos ignorado.

Ahora estos rastros contienen toda la información necesaria para reconstruir el árbol que estamos recorriendo. Así que en lugar de ser un rastro normal, son como una especie de discos de datos que vamos dejando por el camino, ya que contienen mucha más información a parte del camino tomado.

Básicamente, ahora cada rastro es como un sub-árbol cojo. Cuando nos adentramos en un árbol, el rastro almacena toda la información del nodo que nos alejamos exceptuando el sub-árbol que estamos recorriendo. También tenemos que fijarnos en la información que vamos ignorando, por ejemplo, en caso de LeftCrumb sabemos que nos acabamos de desplazar por el sub-árbol izquierdo, así que no guardamos ninguna información de este sub-árbol.

Vamos a modificar el sinónimo de tipo Breadcrumbs para refleje este cambio:

type Breadcrumbs a = [Crumb a]

A continuación vamos modificar las funciones goLeft y goRight para que almacenen en el rastro la información de los caminos que no hemos tomado, en lugar de ignorar esta información como hacíamos antes. Así sería goLeft:

goLeft :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goLeft (Node x l r, bs) = (l, LeftCrumb x r:bs)

Es muy parecida a la versión anterior de goLeft, solo que en lugar de añadir L a la cabeza de la lista de rastros, añadimos un elemento LeftCrumb para representar que hemos tomado el camino izquierdo y además indicamos el nodo desde el que nos hemos desplazado (es decir x) y el camino que no hemos tomado (es decir, el sub-árbol derecho, r).

Fíjate que esta función asume que el árbol en el que nos encontramos no es Empty. Un árbol vacío no tiene ningún sub-árbol, así que si intentamos movernos por un árbol vacío, obtendremos un error a la hora de ajustar los patrones.

goRight es parecido:

goRight :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goRight (Node x l r, bs) = (r, RightCrumb x l:bs)

Ahora somos totalmente capaces de movernos de izquierda a derecha. Lo que aún no podemos hacer es volver por el camino recorrido utilizando la información que indica los nodos padres que hemos recorrido. Aquí tienes la función goUp:

goUp :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goUp (t, LeftCrumb x r:bs) = (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = (Node x l t, bs)

No encontramos en el árbol t y tenemos que comprobar el último Crumb. Si es un LeftCrumb, entonces reconstruimos un nuevo árbol donde t es el sub-árbol izquierdo y utilizamos la información del sub-árbol derecho que no hemos visitado junto al elemento del nodo padre para reconstruir un nuevo Node. Como hemos utilizado el rastro anterior para recrear el nuevo nodo, por decirlo de algún modo, la lista de rastros ya no tiene que contener este último rastro.

Fíjate que esta función genera un error en caso que ya nos encontremos en la cima del árbol. Luego veremos como utilizar la mónada Maybe para representar los posibles fallos de desplazamiento.

Gracias al par formado por Tree a y Breadcrumbs a, tenemos toda la información necesaria para reconstruir el árbol entero y también tenemos señalado un nodo concreto. Este modelo nos permite también movernos fácilmente hacia arriba, izquierda o derecha. Todo par que contenga una parte seleccionada de una estructura y todo la parte que rodea a esa parte seleccionada se llama zipper, esto es así porque se parece a la acción de aplicar zip sobre listas normales de duplas. Un buen sinónimo de tipo sería:

type Zipper a = (Tree a, Breadcrumbs a)

Preferiría llamar al sinónimo de tipos Focus ya que de esta forma es más claro que estamos seleccionando una parte de la estructura, pero el termino zipper se utiliza ampliamente, así que nos quedamos con Zipper.

Manipulando árboles seleccionados

Ahora que nos podemos mover de arriba a abajo, vamos a crear una función que modifique el elemento raíz del sub-árbol que seleccione un zipper.

modify :: (a -> a) -> Zipper a -> Zipper a
modify f (Node x l r, bs) = (Node (f x) l r, bs)
modify f (Empty, bs) = (Empty, bs)

Si estamos seleccionando un nodo, modificamos su elemento raíz con la función f. Si estamos seleccionando un árbol vacío, dejamos éste como estaba. Ahora podemos empezar con un árbol, movernos a donde queramos y modificar un elemento, todo esto mientras mantenemos seleccionado un elemento de forma que nos podemos desplazar fácilmente de arriba a abajo. Un ejemplo:

ghci> let newFocus = modify (\_ -> 'P') (goRight (goLeft (freeTree,[])))

Vamos a la izquierda, luego a la derecha y luego remplazamos el elemento raíz del sub-árbol en el que nos encontramos por 'P'. Se lee mejor si utilizamos -::

ghci> let newFocus = (freeTree,[]) -: goLeft -: goRight -: modify (\_ -> 'P')

Luego podemos desplazarnos hacía arriba y remplazar el elemento por una misteriosa 'X':

ghci> let newFocus2 = modify (\_ -> 'X') (goUp newFocus)

O con -::

ghci> let newFocus2 = newFocus -: goUp -: modify (\_ -> 'X')

Movernos hacia arriba es fácil gracias a que el rastro que vamos dejando que contiene los caminos que no hemos tomado, así que, es como deshacer el camino. Por esta razón, cuando queremos movernos hacia arriba no tenemos que volver a empezar desde la raíz inicial, simplemente podemos volver por el camino que hemos tomado.

Cada nodo posee dos sub-árboles, incluso aunque los dos sub-árboles sean árboles vacíos. Así que si estamos seleccionando un sub-árbol vacío, una cosa que podemos hacer es remplazar un sub-árbol vació por un árbol que contenga un nodo.

attach :: Tree a -> Zipper a -> Zipper a
attach t (_, bs) = (t, bs)

Tomamos un árbol y un zipper y devolvemos un nuevo zipper que tendrá seleccionado el árbol que pasemos como parámetro. Esta función no solo nos permite añadir nodos a las hojas de un árbol, sino que también podemos remplazar sub-árboles enteros. Vamos a añadir un árbol a la parte inferior izquierda de freeTree:

ghci> let farLeft = (freeTree,[]) -: goLeft -: goLeft -: goLeft -: goLeft
ghci> let newFocus = farLeft -: attach (Node 'Z' Empty Empty)

newFocus ahora selecciona un nuevo árbol que ha sido añadido al árbol original. Si utilizáramos goUp para subir por el árbol, veríamos que sería igual que freeTree pero con un nodo adicional 'Z' en su parte inferior izquierda.

Me voy a la cima del árbol, donde el aire está limpio y fresco

Crear una función que seleccione la cima del árbol, independientemente del nodo seleccionado, es realmente fácil:

topMost :: Zipper a -> Zipper a
topMost (t,[]) = (t,[])
topMost z = topMost (goUp z)

Si nuestro rastro está vacío, significa que ya estamos en la cima del árbol, así que solo tenemos que devolver el mismo nodo que está seleccionado. De otro modo, solo tenemos que seleccionar el nodo padre del actual y volver a aplicar de forma recursiva topMost. Ahora podemos dar vueltas por un árbol, ir a la izquierda o a la derecha, aplicar modify o attach para realizar unas cuantas modificaciones, y luego, gracias a topMost, volver a selecciona la raíz principal del árbol y ver si hemos modificado correctamente el árbol.

Seleccionando elementos de la listas

Los zippers se pueden utilizar con casi cualquier tipo de estructura, así que no debería sorprendente que también se puedan utilizar con las listas. Después de todo, las listas son muy parecidas a los árboles. El los árboles un nodo puede tener un elemento (o no) y varios sub-árboles, mientras que en las listas un elemento puede tener una sola sub-lista. Cuando implementamos nuestro propio tipo de listas, definimos el tipo así:

data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)

Si lo comparamos con la definición anterior de los árboles binarios podemos observar como las listas pueden definirse como un árbol que solo posee un sun-árbol.

La lista [1,2,3] es igual que 1:2:3:[]. Está formada por la cabeza de la lista, que es 1 y su cola, que es 2:3:[]. Al mismo tiempo, 2:3:[] está formado por su cabeza, que es 2, y por su cola, que es 3:[]. 3:[] está formado por su cabeza 3 y su cola que es la lista vacía [].

Vamos a crear un zipper para las listas. Para modificar el elemento seleccionado de una lista, podemos mover hacia adelante o hacia atrás (mientras que con los árboles podíamos movernos a la derecha, a la izquierda, y arriba). La parte que seleccionábamos con los árboles era un sub-árbol, a la vez que el rastro que dejábamos cuando avanzábamos. Ahora, ¿qué tendremos que dejar como rastro? Cuando estábamos trabajando con árboles binarios, vimos que el rastro tenía que albergar el elemento raíz de su nodo padre junto a todos los sub-árboles que recorrimos. También teníamos que recordar si habíamos ido por la izquierda o por la derecha. Resumiendo, teníamos que poseer toda la información del nodo que contenía el sub-árbol que estábamos seleccionando.

Las listas son más simples que los árboles, así que no tenemos que recordar si hemos ido por la derecha o por la izquierda, ya que solo podemos avanzar en una dirección. Como solo hay un posible sub-árbol para cada nodo, tampoco tenemos que recordar el camino que tomamos. Parece que lo único que debemos recordar el elemento anterior. Si tenemos una lista como [3,4,5] y sabemos que el elemento anterior es 2, podemos volver atrás simplemente añadiendo dicho elemento a la cabeza de la lista, obteniendo así [2,3,4,5].

Como cada rastro es un elemento, no necesitamos crear un nuevo tipo de datos como hicimos con el tipo de datos Crumb para los árboles:

type ListZipper a = ([a],[a])

La primera lista representa la lista que estamos seleccionando y la segunda lista es la lista de rastros. Vamos a crear las funcionen que avancen y retrocedan por las listas:

goForward :: ListZipper a -> ListZipper a
goForward (x:xs, bs) = (xs, x:bs)

goBack :: ListZipper a -> ListZipper a
goBack (xs, b:bs) = (b:xs, bs)

Cuando avanzamos, seleccionamos la cola de la lista actual y dejamos la cabeza como rastro. Cuando retrocedemos, tomamos el último rastro y lo insertamos al principio de la lista.

Aquí tienes un ejemplo de estas funciones en acción:

ghci> let xs = [1,2,3,4]
ghci> goForward (xs,[])
([2,3,4],[1])
ghci> goForward ([2,3,4],[1])
([3,4],[2,1])
ghci> goForward ([3,4],[2,1])
([4],[3,2,1])
ghci> goBack ([4],[3,2,1])
([3,4],[2,1])

Podemos observar que el rastro de una listas no es nada más que la parte invertida de la lista que hemos dejado atrás. El elemento que dejamos atrás siempre pasa a formar parte de la cabeza de los rastros, así que es fácil movernos hacía atrás tomando simplemente el primer elemento de los rastros y añadiéndolo a la lista que tenemos seleccionada.

Si estamos creando un editor de texto, podemos utilizar una lista de cadenas para representar las líneas de texto del fichero que estemos editando, luego podemos utilizar un zipper de forma que sepamos donde se encuentra el cursor. El hecho de utilizar los zipper también facilitaría la introducción de líneas de texto nuevas en cualquier parte del texto o barrar líneas existentes.

Un sistema de ficheros simple

Ahora que sabemos como funcionan los zippers, vamos utilizar un árbol para representar un sistema de ficheros y luego crearemos un zipper para ese sistema, lo cual nos permitirá movernos entre los directorios de la misma forma que hacemos nosotros mismos.

Si tomamos una versión simplificada de los sistemas de ficheros jerárquicos, podemos observar que básicamente están formados por ficheros y directorios. Los ficheros son las unidades de información y poseen un nombre, mientras que los directorios se utilizan para organizar estos ficheros y pueden contener tanto ficheros como otros directorios. Así que vamos a decir que un objeto de sistema de ficheros es o bien un fichero, que viene acompañado de un nombre y unos datos, o bien un directorio, que viene acompañado de un nombre y un conjunto de objetos que pueden ser tanto ficheros como directorios. Aquí tienes el tipo de datos para este sistema junto un par de sinónimos de tipo:

type Name = String
type Data = String
data FSItem = File Name Data | Folder Name [FSItem] deriving (Show)

Cada fichero viene con dos cadenas, una representa su nombre y otra sus contenidos. Cada directorio viene con una cadena que representa su nombre y un lista de objetos. Si la lista está vacía, entonces tenemos un directorio vacío.

Aquí tienes un ejemplo:

myDisk :: FSItem
myDisk =
    Folder "root"
        [ File "goat_yelling_like_man.wmv" "baaaaaa"
        , File "pope_time.avi" "god bless"
        , Folder "pics"
            [ File "ape_throwing_up.jpg" "bleargh"
            , File "watermelon_smash.gif" "smash!!"
            , File "skull_man(scary).bmp" "Yikes!"
            ]
        , File "dijon_poupon.doc" "best mustard"
        , Folder "programs"
            [ File "fartwizard.exe" "10gotofart"
            , File "owl_bandit.dmg" "mov eax, h00t"
            , File "not_a_virus.exe" "really not a virus"
            , Folder "source code"
                [ File "best_hs_prog.hs" "main = print (fix error)"
                , File "random.hs" "main = print 4"
                ]
            ]
        ]

En verdad es el contenido de mi disco duro en este momento.

Un zipper para el sistema de ficheros

Ahora que tenemos un sistema de ficheros, lo que necesitamos es un zipper de forma que podamos desplazarnos, crear, modificar o eliminar ficheros al vez que directorios. De la misma forma que con los árboles binarios y las listas, vamos a ir dejando un rastro que contenga todas las cosas que no hemos visitado. Como ya hemos dicho, cada rastro debe ser una especie de nodo, solo que no debe contener el sub-árbol que estamos seleccionando para no repetir información. También tenemos que tener en cuenta la posición en la que nos encontramos, de forma que podamos volver atrás.

En este caso en particular, el rastro será algo parecido a un directorio, solo que no debe contener el directorio en el que estamos ¿Y porqué no un fichero? Te estarás preguntando. Bueno, porque una vez hemos seleccionado un fichero, no podemos avanzar en el sistema de ficheros, así que no tiene mucho sentido dejar algo en el rastro que diga que venimos de un fichero. Un fichero es algo parecido a un árbol vacío.

Si nos encontramos en el directorio "root" y queremos seleccionar el fichero "dijon_poupon.doc", ¿qué debería contener el rastro? Bueno, debería contener el nombre del directorio padre junto con todos los elementos anteriores al fichero que estamos seleccionando más los elementos posteriores. Así que lo que necesitamos es un Name y dos listas de objetos. Manteniendo dos listas separadas de elementos, una con los elementos anteriores y otra con los elementos posteriores, sabremos exactamente que seleccionar si volvemos atrás.

Aquí tenemos el tipo rastro para nuestro sistema de ficheros:

data FSCrumb = FSCrumb Name [FSItem] [FSItem] deriving (Show)

Y aquí nuestro sinónimo de tipo para zipper:

type FSZipper = (FSItem, [FSCrumb])

Volver atrás por esta jerarquía es muy fácil. Solo tenemos que tomar el último elemento del rastro y seleccionar un nuevo elemento a partir del objeto actualmente seleccionado y del rastro. Así:

fsUp :: FSZipper -> FSZipper
fsUp (item, (FSCrumb name ls rs):bs) = (Folder name (ls ++ [item] ++ rs), bs)

Como el rastro contiene el nombre del directorio padre, así como los elementos anteriores al objeto seleccionado (es decir, ls) y los posteriores (rs), retroceder es muy sencillo.

¿Y si queremos avanzar por el sistema de ficheros? Si estamos en "root" y queremos seleccionar "dijon_poupon.doc", el rastro contendrá el nombre "root" junto con los elementos que preceden a "dijon_poupon.doc" y los que van después.

Aquí tienes una función que, dado un nombre, selecciona el fichero o directorio que este contenido en el directorio actual:

import Data.List (break)

fsTo :: Name -> FSZipper -> FSZipper
fsTo name (Folder folderName items, bs) =
    let (ls, item:rs) = break (nameIs name) items
    in  (item, FSCrumb folderName ls rs:bs)

nameIs :: Name -> FSItem -> Bool
nameIs name (Folder folderName _) = name == folderName
nameIs name (File fileName _) = name == fileName

fsTo toma un Name y un FSZipper y devuelve un nuevo FSZipper que tendrá seleccionado el fichero con el nombre dado. El dicho debe estar en el directorio actual. Esta función no busca el fichero sobre todos los directorios, solo con el directorio actual.

Primero utilizamos break par dividir la lista de elementos en un lista con los elementos anteriores al fichero que estamos buscando y en una lista con los que van después. Si recuerdas, break toma un predicado y una lista y devuelve una dupla que contiene dos listas. La primera lista en la dupla contiene los elementos en los que el predicado no se cumplió. Luego, una vez encuentra un elemento que cumple el predicado, introduce ese elemento y el resto de la lista en la segunda componente de la dupla. Hemos creado un función auxiliar llamada nameIs que toma un nombre y un objeto del sistema de ficheros y devuelve True si coinciden los nombres.

Ahora, ls es una lista que contiene los elementos que preceden al objetos que estamos buscando, item es dicho objeto y rs es la lista de objetos que viene después del objeto en cuestión. Con todo esto, solo tenemos que devolver el objeto que obtuvimos de break y crear un rastro con toda la información requerida.

Fíjate que si el nombre que estamos buscando no está en el directorio actual, el patrón item:rs no se ajustará y por lo tanto obtendremos un error. También, si el elemento seleccionado no es directorio, es decir, es un fichero, también obtendremos un error y el programa terminará.

Ahora ya podemos movernos por el sistema de ficheros. Vamos a partir de la raíz y recorrer el sistema hasta el fichero "skull_man(scary).bmp":

ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsTo "skull_man(scary).bmp"

newFocus es ahora un zipper que selecciona el fichero "skull_man(scary).bmp". Vamos a obtener el primer componente del zipper (el objeto seleccionado) y comprobar si es verdad:

ghci> fst newFocus
File "skull_man(scary).bmp" "Yikes!"

Vamos a volver atrás y seleccionar su fichero vecino “watermelon_smash.gif”:

ghci> let newFocus2 = newFocus -: fsUp -: fsTo "watermelon_smash.gif"
ghci> fst newFocus2
File "watermelon_smash.gif" "smash!!"

Manipulando el sistema de ficheros

Ahora que ya podemos navegar por el sistema de ficheros, manipular los elementos es muy fácil. Aquí tienes un función que renombra el fichero o directorio actual:

fsRename :: Name -> FSZipper -> FSZipper
fsRename newName (Folder name items, bs) = (Folder newName items, bs)
fsRename newName (File name dat, bs) = (File newName dat, bs)

Podemos renombrar el directorio "pics" a "cspi":

ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsRename "cspi" -: fsUp

Nos hemos metido en el directorio "pics", lo hemos renombrado, y luego hemos vuelto.

¿Qué tal una función que crea un nuevo elemento en el directorio actual?

fsNewFile :: FSItem -> FSZipper -> FSZipper
fsNewFile item (Folder folderName items, bs) =
    (Folder folderName (item:items), bs)

Facilísimo. Ten en cuenta que esta función fallara si intentamos añadir un elemento a algo que no sea un directorio.

Vamos a añadir un fichero a nuestro directorio "pics" y luego volver atrás:

ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsNewFile (File "heh.jpg" "lol") -: fsUp

Lo realmente interesante de este método es que cuando modificamos el sistema de ficheros, en realidad no modifica ese mismo sistema, si no que devuelve uno totalmente nuevo. De este modo, podremos acceder al sistema de ficheros antiguo (myDisk en este caso) y también al nuevo (el primer componente de newFocus). Así que gracias a los zippers, obtenemos automáticamente copias de diferentes versiones, de forma que siempre podremos referenciar a versiones antiguas aunque lo hayamos modificado. Esto no es una propiedad única de los zippers, si no de todas las estructuras de datos de Haskell ya que son inmutables. Sin embargo con los zippers, ganamos la habilidad de recorrer y almacenar eficientemente estas estructuras de datos.

Vigila tus pasos

Hasta ahora, cuando recorríamos estructuras de datos, ya sean árboles binarios, listas o sistemas de ficheros, no nos preocupábamos de sí tomábamos un paso en falso y nos salíamos de la estructura. Por ejemplo, la función goLeft toma un zipper de un árbol binario y mueve el selector al árbol izquierdo:

goLeft :: Zipper a -> Zipper a
goLeft (Node x l r, bs) = (l, LeftCrumb x r:bs)

Pero, ¿y si el árbol en el que nos encontramos está vacío? Es decir, no es un Node si no un Empty. En este caso, obtendremos un error de ejecución ya que el ajuste de patrones fallará ya que no hay ningún patrón que se ajuste a árboles vacíos, lo cuales no contienen ningún sub-árbol. Hasta ahora, simplemente hemos asumido que nunca íbamos a intentar seleccionar el sub-árbol izquierdo de un árbol vacío ya que dicho sub-árbol no existe. De todos modos, ir al sub-árbol izquierdo de un árbol vacío no tiene mucho sentido, y hasta ahora no nos hemos preocupado de ello.

O, ¿qué pasaría si estamos en la raíz de un árbol y no tenemos ningún rastro e intentamos continuar hacía arriba? Ocurriría lo mismo. Parece que cuando utilizamos los zipper, cada paso que demos puede ser el último (reproducir música siniestra aquí). En otras palabras, cada movimiento puede ser un éxito, pero también fallo. Sí, es la ultima vez que te lo pregunto, y se que lo estás deseando, ¿a qué te recuerda esto? Por supuesto, ¡mónadas! en concreto la mónada Maybe que se encarga de contextos con posibles fallos.

Vamos a utilizar la mónada Maybe para añadir el contexto de un posible fallo a nuestro pasos. Vamos a tomar las funciones que ya funcionan con el zipper de árboles binarios y vamos a convertirlas en funciones monádicas. Primero, vamos a añadir el contexto de un posible fallo a goLeft y goRight. Hasta ahora, el fallo de una función se reflejaba en su resultado y no va ser distinto aquí.

goLeft :: Zipper a -> Maybe (Zipper a)
goLeft (Node x l r, bs) = Just (l, LeftCrumb x r:bs)
goLeft (Empty, _) = Nothing

goRight :: Zipper a -> Maybe (Zipper a)
goRight (Node x l r, bs) = Just (r, RightCrumb x l:bs)
goRight (Empty, _) = Nothing

¡Genial! Ahora si intentamos dar un paso a la izquierda por un árbol vacío obtendremos un Nothing.

ghci> goLeft (Empty, [])
Nothing
ghci> goLeft (Node 'A' Empty Empty, [])
Just (Empty,[LeftCrumb 'A' Empty])

Parece que funciona ¿Y si vamos hacia arriba? Aquí el problema está en si queremos ir hacía arriba y no hay ningún rastro más, ya que esta situación indica que nos encontramos en la cima del árbol. Esta es la función goUp que lanza un error si nos salimos de los límites:

goUp :: Zipper a -> Zipper a
goUp (t, LeftCrumb x r:bs) = (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = (Node x l t, bs)

Y esta la versión modificada:

goUp :: Zipper a -> Maybe (Zipper a)
goUp (t, LeftCrumb x r:bs) = Just (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = Just (Node x l t, bs)
goUp (_, []) = Nothing

Si tenemos un rastro no hay ningún problema y podemos devolver un nuevo nodo seleccionado. Si embargo, si no hay ningún rastro devolvemos un fallo.

Antes estas funciones tomaban zippers y devolvían zippers, por lo tanto podíamos encadenarlas así:

gchi> let newFocus = (freeTree,[]) -: goLeft -: goRight

Ahora, en lugar de devolver un Zipper a, devuelven Maybe (Zipper a), así que no podemos encadenar las funciones de este modo. Tuvimos un problema similar cuando estábamos con nuestro buen amigo el funambulista, en el capítulo de las mónadas. Él también tomaba un paso detrás de otro, y cada uno de ellos podía resultar en un fallo porque siempre podían aterrizar un grupo de pájaros en lado y desequilibrar la barra.

Ahora el problema lo tenemos nosotros, que somos los que estamos recorriendo el árbol. Por suerte, aprendimos mucho de Pierre y de lo que hizo: cambiar la aplicación normal de funciones por la monádica, utilizando >>=, que toma un valor en un contexto (en nuestro caso, Maybe (Zipper a), que representa el contexto de un posible fallo) y se lo pasa a un función de forma que se mantenga el significado del contexto. Así que al igual que nuestro amigo, solo tenemos que intercambiar -: por >>=. Mira:

ghci> let coolTree = Node 1 Empty (Node 3 Empty Empty)
ghci> return (coolTree,[]) >>= goRight
Just (Node 3 Empty Empty,[RightCrumb 1 Empty])
ghci> return (coolTree,[]) >>= goRight >>= goRight
Just (Empty,[RightCrumb 3 Empty,RightCrumb 1 Empty])
ghci> return (coolTree,[]) >>= goRight >>= goRight >>= goRight
Nothing

Hemos utilizado return para introducir un zipper en un valor Just y luego hemos utilizado >>= para pasar ese valor a la función goRight. Primero, creamos un árbol que tiene en su rama izquierda un sub-árbol vacío y en su rama derecha dos sub-árbol vacíos. Cuando intentamos ir por la rama derecha, el movimiento tiene éxito porque la operación tiene sentido. Volver a ir a la derecha también está permitido, acabamos seleccionando un árbol vacío. Pero si damos un paso más por tercera vez no tendrá sentido, porque no podemos visitar la rama derecha o izquierda de un sub-árbol vacío, por la tanto obtenemos Nothing.

Ahora ya tenemos equipadas nuestras funciones con una red de seguridad que nos salvará si nos caemos. Momento metafórico.

El sistema de fichero también posee un montón de casos donde podría fallar, como intentar seleccionar un fichero o un directorio que no existe. Como último ejercicio, si quieres claro, puedes intentar añadir a estas funciones el contexto de un posibles fallos utilizando la mónada Maybe.